十進BASICによる円周率

はじめに

円周率は、円周と直径の比の値であり、昔から多くの人々の興味を引いてきました。このページでは、十進BASICを用いた円周率の計算について紹介したいと思います。このBASICには十進1000桁モードという機能があり、有効数字1000桁の計算を実行することができます。ただし、誤差の関係で最後の数桁はあっていないかもしれません。

漸化式による円周率計算

最初に、漸化式で表すことができる次の公式を見てみましょう。

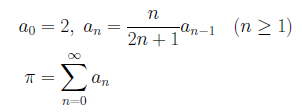
この公式を、十進BASICのプログラムにしてみます。十進1000桁モードで実行してみてください。

PiEuler.BAS

   1: ! 十進1000桁モード
   2: OPTION ARITHMETIC DECIMAL_HIGH
   3: ! 繰り返し回数
   4: LET iter = 3500
   5: 
   6: ! 初期値
   7: LET a = 2
   8: LET s = a
   9: PRINT USING "####":0;
  10: PRINT s
  11: 
  12: ! 繰り返し
  13: FOR i = 1 TO iter
  14:    LET  a = a * i / (2 * i + 1)
  15:    LET  s = s + a
  16:    PRINT USING "####":i;
  17:    PRINT s
  18: NEXT i
  19: END

類似の式で、より収束の速い公式もあります。

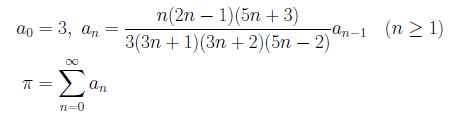
PiGosper.BAS

   1: ! 十進1000桁モード
   2: OPTION ARITHMETIC DECIMAL_HIGH
   3: ! 繰り返し回数
   4: LET iter = 900
   5: 
   6: ! 初期値
   7: LET a = 3
   8: LET s = a
   9: PRINT USING "###":0;
  10: PRINT s
  11: 
  12: ! 繰り返し
  13: FOR i = 1 TO iter
  14:    LET a = a * i * (2 * i - 1) * (5 * i + 3) / 3
  15:    LET a = a / (3 * i + 1) / (3 * i + 2) / (5 * i - 2)
  16:    LET s = s + a
  17:    PRINT USING "###":i;
  18:    PRINT s
  19: NEXT i
  20: END

また、円周率の逆数を与える漸化式もあります。

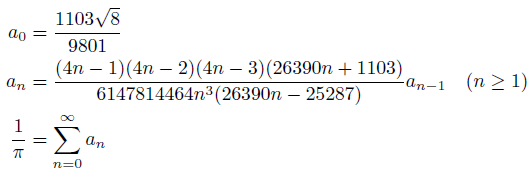
PiRamanujan.BAS

   1: ! 十進1000桁モード
   2: OPTION ARITHMETIC DECIMAL_HIGH
   3: ! 繰り返し回数
   4: LET iter = 130
   5: 
   6: ! 初期値
   7: LET a = 1103 * SQR(8) / 9801
   8: LET s = a
   9: PRINT USING "###":0;
  10: PRINT 1 / s
  11: 
  12: ! 繰り返し
  13: FOR i = 1 TO iter
  14:    LET  a = a * (4 * i - 1) * (4 * i - 2) * (4 * i - 3) * (26390 * i + 1103)
  15:    LET  a = a / 6147814464 / i^3 / (26390 * i - 25287)
  16:    LET  s = s + a
  17:    PRINT USING "###":i;
  18:    PRINT 1 / s
  19: NEXT i
  20: END

参考文献

1. 小林昭七、円の数学、裳華房、1999、ISBN 4-7853-1516-4
2. 楠葉隆徳、林隆夫、矢野道雄、インド数学研究--数列、円周率、三角法--、恒星社厚生閣、1997、ISBN 4-7699-6841-5
3. 数学文化001　特集=円周率π、日本評論社、2003、ISBN 4-535-60231-X
4. 奥村晴彦、首藤一幸、杉浦方紀、土村展之、都留和生、細田隆之、松井吉光、光成滋生、Javaによるアルゴリズム事典、技術評論社、2003、ISBN 4-7741-1729-3
5. J.-P. ドゥラエ、畑正義訳、π-魅惑の数、朝倉書店、2001、ISBN 978-4-254-11086-9
6. 戸川隼人、新装版UNIXワークステーションによる科学技術計算ハンドブック　基礎篇C言語版、サイエンス社、1992、ISBN 4-7819-0868-3
7. 森口繁一、計算数学夜話--数値で学ぶ高等数学--、日本評論社、1978、ISBN 4-535-78117-6
8. 一松信、教室に電卓をII、海鳴社、1981
9. 森本光生、パソコンによる解析入門、放送大学教育振興会、1995、ISBN 4-595-86421-3
10. 森本光生、パソコンによる解析学、放送大学教育振興会、1999、ISBN 4-595-56444-9
11. 伊理正夫、藤野和建、数値計算の常識、共立出版、1985、ISBN 4-320-01343-3
12. 藤野清次、数値計算の基礎--数値解法を中心に--、サイエンス社、1998、ISBN 4-7819-0861-6
13. 二宮市三編、数値計算のつぼ、共立出版、2004、ISBN 4-320-12088-4
14. 二宮市三編、数値計算のわざ、共立出版、2006、ISBN 4-320-01803-6
15. 寺澤順、πと微積分の23話、日本評論社、2006、ISBN 4-535-78531-7
16. 竹之内脩、伊藤隆、π--πの計算　アルキメデスから現代まで--、共立出版、2007、ISBN 978-4-320-01834-1
17. 小川束、平野葉一、講座数学の考え方24 数学の歴史 和算と西欧数学の発展、朝倉書店、2003、ISBN 4-254-11604-7
18. 江沢洋、岩波講座 応用数学 [方法5] 漸近解析、岩波書店、1995、ISBN 4-00-010804-2
19. 杉原正顯、室田一雄、数値計算法の数理、岩波書店、1994、ISBN 4-00-005518-6
20. 右田剛史、天野晃、浅田尚紀、藤野清次、級数の再帰的集約による多倍長数の計算法とπの計算への応用、情報処理学会論文誌、40(1999),no.12,4193--4200
21. 上野健爾、円周率πをめぐって、日本評論社、1999、ISBN 4-535-60840-7
22. 横塚啓之、円理史研究の新展開　最近の建部研究の成果、数学の楽しみ2006夏　関孝和と建部賢弘、日本評論社、2006、ISBN 4-535-60319-7
23. 津田孝夫、モンテカルロ法とシミュレーション　＜三訂版＞、培風館、1995、ISBN 4-563-00878-8
24. レオンハルト・オイラー著、高瀬正仁訳、オイラーの無限解析、海鳴社、2001、ISBN 4-87525-202-1
25. 野崎昭弘、πとeの連分数展開とその数値計算法、大妻女子大学紀要　社会情報系　社会情報学研究、15 (2006), 251--255
26. Jorg Arndt, Christoph Haenel, π Unleashed, Springer, 2001, ISBN 3-540-66572-2
27. Konrad Knopp, Theory and application of infinite series, Dover, 1999, ISBN 0-486-66165-2
28. Jonathan M. Borwein, Peter B. Borwein, Pi and the AGM, Wiley-Interscience, 1998, ISBN 0-471-31515-X
29. Avram Sidi, Practical Extrapolation Methods: Theory and Applications, Cambridge Unversity Press, 2002, ISBN 978-0-521-66159-1
30. P.Eymard, J.-P.Lafon, The number π, American Mathematical Society, 2004, ISBN 0-8218-3246-8
31. Ernst Joachim Weniger, Nonlinear sequence transformations for the acceleration of convergence and the summation of divergent series, Computer Physics Reports, 10 (1989) 189--371
32. Stanley Rabinowitz, Stan Wagon, A Spigot Algorithm for the Digits of π, Amer. Math. Monthly 102 (1995), no.3, 195--203
33. Jeremy Gibbons, Unbounded Spigot Algorithms for the Digits of Pi, Amer. Math. Monthly 113 (2006), no.4, 318--328
34. Claude Brezinski, Some New Convergence Acceleration Methods, Math. Comput. 39 (1982), no.159, 133--145
35. Henri Cohen, Fernando Rodriguez Villegas, Don Zagier, Convergence Acceleration of Alternating Series, Experimental Math. 9 (2000), no.1, 3--12
36. R.Thukral, Development of the Levin-type algorithms for accelerating convergence of sequences, Nonlinear Analysis 64 (2006), 229--241
37. R.Thukral, A new method for accelerating convergence of alternating series, Appl. Math. Comput. 187 (2007), no.2, 1502--1510
38. G.M.Phillips, Amer. Math. Monthly 91 (1984), no.2, 108--114
39. J.Mc Laughlin, N.J.Wyshinski, Real Numbers with Polynomial Continued Fraction Expansions, Acta Arith., 116 (2005),no.1, 63--79
40. 円周率と黄金比
41. 数学研究ノート by Sugimoto
42. L.Lorentzen, H.Waadeland, Continued Fractions with Applications, North-Holland, 1992 ISBN 0-444-89265-6
43. A.Cuyt, V.Brevik Petersen, B.Verdonk, H.Waadeland, Continued Fractions for Special Functions, Springer, 2008, ISBN 978-1-4020-6948-2
44. L.Lorentzen, H.Waadeland, Continued Fractios Second Edition, Vol.1:Convergence Theory, World Scientific Publications, 2008, ISBN 978-90-78677-07-9
45. L.A.Lyusternik, A.R.Yanpol'skii, Functions, limits, Series, Continued Fractions, Pergamon Press, 1965
46. S.Khrushchev, On Euler's differential methods for continued fractions, Electr. Trans. Numer. Anal. Kent State Univ. 25 (2006), 178--200