モンテカルロ法による円周率計算

はじめに

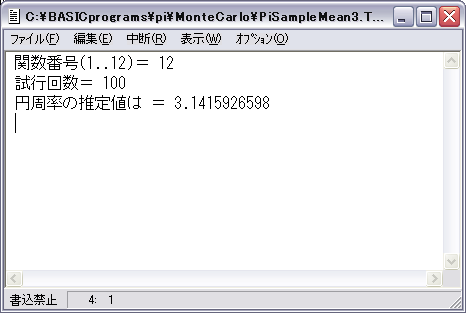
モンテカルロ法によって円周率を求めてみます。一般に精度が悪いと思われがちですが、計算を工夫することによって、精度を上げることができます。次に、後述する十進BASICのプログラム「PiSampleMean3.BAS」を実行したときの結果の一例を表示してみます。試行回数が100回と少ないにも拘らず、小数点以下8桁まで合っています。

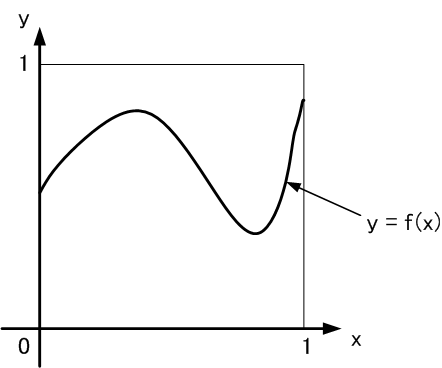
以下、順を追って説明することにします。まず、f(x)を、0≤x≤1において0≤f(x)≤1であるような関数とします。特に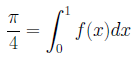となる関数ｆ（ｘ）が知られています。

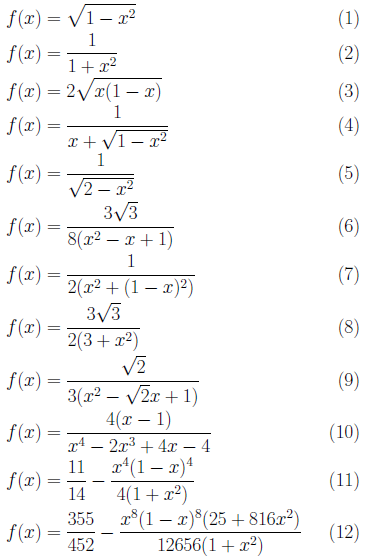
これらの関数を用い、いくつかの手法について説明いたします。ぜひ十進BASICのプログラムを実行してみてください。

当たり外れのモンテカルロ法

まず、当たり外れのモンテカルロ法(Hit-or-miss Monte Carlo)について説明します。ξ , ηを区間[0,1]に一様分布する乱数とします。このとき点(ξ , η)が、対象となる関数y=f(x)の下側にくる回数をn'、総試行回数をnとしたとき、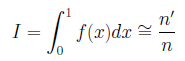となります。

十進BASICのプログラムを次に示します。

PiDartBoard.BAS

   1: !
   2: ! モンテカルロ法による円周率の計算
   3: ! 当たり外れのモンテカルロ法
   4: !
   5: 
   6: ! 初期設定
   7: SET POINT STYLE 1
   8: SET WINDOW -0.2,1.2,-0.2,1.2
   9: DRAW grid
  10: RANDOMIZE
  11: 
  12: ! 外部定義関数の宣言
  13: DECLARE EXTERNAL FUNCTION fnc
  14: 
  15: ! 関数番号の入力
  16: INPUT PROMPT "関数番号(1..12)＝ " : FuncNo
  17: LET  FuncNo = INT(FuncNo)
  18: IF FuncNo < 1 THEN LET  FuncNo = 1
  19: IF FuncNo > 12 THEN LET  FuncNo = 12
  20: 
  21: ! 関数を描く
  22: FOR t = 0 TO 1 STEP 0.01
  23:    PLOT LINES: t, fnc(t, FuncNo);
  24: NEXT t
  25: PLOT LINES
  26: 
  27: INPUT PROMPT "試行回数＝ ": n
  28: LET hit = 0
  29: FOR i = 1 TO n
  30:    LET x = RND  !乱数で点を発生させる
  31:    LET y = RND
  32:    IF y <= fnc(x, FuncNo) THEN !点が関数の下側ならば
  33:       LET hit = hit + 1        !下側の点の数を1増やし
  34:       SET POINT COLOR 2        !点の色を青にする
  35:    ELSE                        !点が上側ならば
  36:       SET POINT COLOR 1        !点の色を黒にする
  37:    END IF
  38:    PLOT POINTS :x,y            !点を打つ
  39: NEXT i
  40: 
  41: LET p = hit / n
  42: 
  43: PRINT "下側の点の数は ＝";hit
  44: PRINT USING "円周率の推定値は ＝ %.#######":4 * p
  45: END
  46: 
  47: EXTERNAL FUNCTION fnc(x, FuncNo)
  48: SELECT CASE FuncNo
  49: CASE 1
  50:    LET  fnc = SQR(1 - x^2)
  51: CASE 2
  52:    LET  fnc = 1 / (1 + x^2)
  53: CASE 3
  54:    LET  fnc = 2 * SQR(x * (1 - x))
  55: CASE 4
  56:    LET  fnc = 1 / (x + SQR(1 - x^2))
  57: CASE 5
  58:    LET  fnc = 1 / SQR(2 - x^2)
  59: CASE 6
  60:    LET  fnc = 3 * SQR(3) / 8 /(x^2 - x + 1)
  61: CASE 7
  62:    LET  fnc = 1 / 2 / (x^2 + (1 - x)^2)
  63: CASE 8
  64:    LET  fnc = 3 * SQR(3) / 2 / (3 + x^2)
  65: CASE 9
  66:    LET  fnc = SQR(2) / 3 / (x^2 - SQR(2)*x + 1)
  67: CASE 10
  68:    LET  fnc = 4 * (x - 1) / (x^4 - 2 * x^3 + 4 * x - 4)
  69: CASE 11
  70:    LET  fnc = 11 / 14 - x^4 * (1 - x)^4 / 4 / (1 + x^2)
  71: CASE 12
  72:    LET fnc = 355 / 452 - x^8 * (1 - x)^8 * (25 + 816 * x^2) / 12656 / (1 + x^2)
  73: END SELECT
  74: END FUNCTION

標本平均モンテカルロ法

標本平均モンテカルロ法(Sample Mean Monte Carlo)あるいは入門的モンテカルロ法(crude Monte Carlo)として知られている方法について紹介いたします。まず、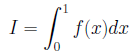の評価を考えます。ξを区間[0,1]に一様分布する乱数とし、p(x)を

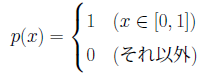
となるような確率密度とすると、期待値E[f(ξ)]は、

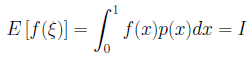
となります。乱数をn個(ξ₁...ξ_n)発生させたとき、Iは、

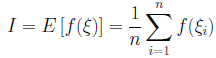
となります。十進BASICのプログラムを次に示します。

PiSampleMean.BAS

   1: !
   2: ! モンテカルロ法による円周率の計算
   3: ! 標本平均モンテカルロ法
   4: !
   5: 
   6: ! 初期設定
   7: SET POINT STYLE 1
   8: SET WINDOW -0.2,1.2,-0.2,1.2
   9: DRAW grid
  10: RANDOMIZE
  11: 
  12: ! 外部定義関数の宣言
  13: DECLARE EXTERNAL FUNCTION fnc
  14: 
  15: ! 関数番号の入力
  16: INPUT PROMPT "関数番号(1..12)＝ " : FuncNo
  17: LET  FuncNo = INT(FuncNo)
  18: IF FuncNo < 1 THEN LET  FuncNo = 1
  19: IF FuncNo > 12 THEN LET  FuncNo = 12
  20: 
  21: ! 関数を描く
  22: FOR t = 0 TO 1 STEP 0.01
  23:    PLOT LINES: t, fnc(t, FuncNo);
  24: NEXT t
  25: PLOT LINES
  26: 
  27: INPUT PROMPT "試行回数＝ ": n
  28: LET sum = 0
  29: LET sumsq = 0
  30: FOR i = 1 TO n
  31:    LET x = RND                 !乱数で点を発生させる
  32:    LET y = fnc(x, FuncNo)      !yの値を計算する
  33:    LET sum = sum + y
  34:    SET LINE COLOR INT(RND * 8) !線の色をランダムに選ぶ
  35:    PLOT LINES :x,0;x,y         !線を引く
  36: NEXT i
  37: 
  38: LET mean = sum / n
  39: 
  40: PRINT USING "円周率の推定値は ＝ %.##########":4 * mean
  41: END
  42: 
  43: EXTERNAL FUNCTION fnc(x, FuncNo)
  44: SELECT CASE FuncNo
  45: CASE 1
  46:    LET  fnc = SQR(1 - x^2)
  47: CASE 2
  48:    LET  fnc = 1 / (1 + x^2)
  49: CASE 3
  50:    LET  fnc = 2 * SQR(x * (1 - x))
  51: CASE 4
  52:    LET  fnc = 1 / (x + SQR(1 - x^2))
  53: CASE 5
  54:    LET  fnc = 1 / SQR(2 - x^2)
  55: CASE 6
  56:    LET  fnc = 3 * SQR(3) / 8 /(x^2 - x + 1)
  57: CASE 7
  58:    LET  fnc = 1 / 2 / (x^2 + (1 - x)^2)
  59: CASE 8
  60:    LET  fnc = 3 * SQR(3) / 2 / (3 + x^2)
  61: CASE 9
  62:    LET  fnc = SQR(2) / 3 / (x^2 - SQR(2)*x + 1)
  63: CASE 10
  64:    LET  fnc = 4 * (x - 1) / (x^4 - 2 * x^3 + 4 * x - 4)
  65: CASE 11
  66:    LET  fnc = 11 / 14 - x^4 * (1 - x)^4 / 4 / (1 + x^2)
  67: CASE 12
  68:    LET fnc = 355 / 452 - x^8 * (1 - x)^8 * (25 + 816 * x^2) / 12656 / (1 + x^2)
  69: END SELECT
  70: END FUNCTION

標本平均モンテカルロ法(主部の分離による高精度化)

モンテカルロ法には、精度を上げるための手法がいくつか知られています。最初に紹介しますのは、主部の分離と呼ばれる方法です。y=f(x)に対し、f(x)から別の(積分を計算しやすい)分かっている関数g(x)を差し引くことを考えます。このとき、g(x)〜f(x)となるようにg(x)を選びます。ここで、

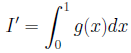
とします。すると

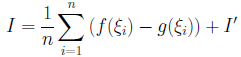
により、Iを求めることができます。次に、先に挙げた12のf(x)に対応するg(x)の例を示します。

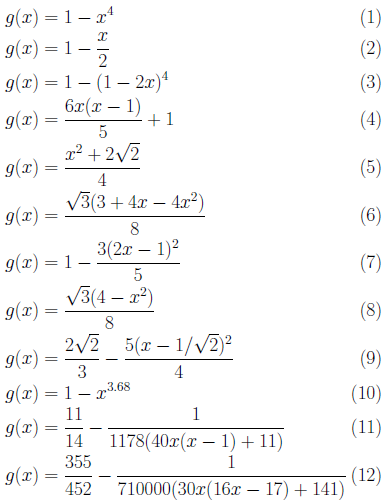
これらのg(x)の積分I'は、次のようになります。

十進BASICのプログラムを次に示します。

PiSampleMean2.BAS

   1: !
   2: ! モンテカルロ法による円周率の計算
   3: ! 標本平均モンテカルロ法(主部の分離による高精度化)
   4: !
   5: 
   6: ! 初期設定
   7: SET POINT STYLE 1
   8: SET WINDOW -0.2,1.2,-0.2,1.2
   9: DRAW grid
  10: RANDOMIZE
  11: 
  12: ! 外部定義関数の宣言
  13: DECLARE EXTERNAL FUNCTION fnc
  14: DECLARE EXTERNAL FUNCTION fncg
  15: DECLARE EXTERNAL FUNCTION S
  16: 
  17: ! 関数番号の入力
  18: INPUT PROMPT "関数番号(1..12)＝ " : FuncNo
  19: LET  FuncNo = INT(FuncNo)
  20: IF FuncNo < 1 THEN LET  FuncNo = 1
  21: IF FuncNo > 12 THEN LET  FuncNo = 12
  22: 
  23: ! 関数を描く
  24: FOR t = 0 TO 1 STEP 0.01
  25:    PLOT LINES: t, fnc(t, FuncNo);
  26: NEXT t
  27: PLOT LINES
  28: SET LINE COLOR 2
  29: FOR t = 0 TO 1 STEP 0.01
  30:    PLOT LINES: t, fncg(t, FuncNo);
  31: NEXT t
  32: PLOT LINES
  33: 
  34: INPUT PROMPT "試行回数＝ ": n
  35: LET sum = 0
  36: LET sumsq = 0
  37: FOR i = 1 TO n
  38:    LET x = RND                 !乱数で点を発生させる
  39:    LET y = fnc(x, FuncNo) - fncg(x, FuncNo) !yの値を計算する
  40:    LET sum = sum + y
  41:    SET LINE COLOR INT(RND * 8) !線の色をランダムに選ぶ
  42:    PLOT LINES :x,fnc(x, FuncNo);x,fncg(x, FuncNo)         !線を引く
  43:    !   PLOT LINES :x,0;x,y         !線を引く
  44: NEXT i
  45: 
  46: LET mean = sum / n
  47: 
  48: PRINT USING "円周率の推定値は ＝ %.##########":4 * (mean + S(FuncNo))
  49: END
  50: 
  51: EXTERNAL FUNCTION fnc(x, FuncNo)
  52: SELECT CASE FuncNo
  53: CASE 1
  54:    LET  fnc = SQR(1 - x^2)
  55: CASE 2
  56:    LET  fnc = 1 / (1 + x^2)
  57: CASE 3
  58:    LET  fnc = 2 * SQR(x * (1 - x))
  59: CASE 4
  60:    LET  fnc = 1 / (x + SQR(1 - x^2))
  61: CASE 5
  62:    LET  fnc = 1 / SQR(2 - x^2) 
  63: CASE 6
  64:    LET  fnc = 3 * SQR(3) / 8 /(x^2 - x + 1)
  65: CASE 7
  66:    LET  fnc = 1 / 2 / (x^2 + (1 - x)^2)
  67: CASE 8
  68:    LET  fnc = 3 * SQR(3) / 2 / (3 + x^2)
  69: CASE 9
  70:    LET  fnc = SQR(2) / 3 / (x^2 - SQR(2)*x + 1)
  71: CASE 10
  72:    LET  fnc = 4 * (x - 1) / (x^4 - 2 * x^3 + 4 * x - 4)
  73: CASE 11
  74:    LET  fnc = 11 / 14 - x^4 * (1 - x)^4 / 4 / (1 + x^2)
  75: CASE 12
  76:    LET  fnc = 355 / 452 - x^8 * (1 - x)^8 * (25 + 816 * x^2) / 12656 / (1 + x^2)
  77: END SELECT
  78: END FUNCTION
  79: 
  80: EXTERNAL FUNCTION fncg(x, FuncNo)
  81: SELECT CASE FuncNo
  82: CASE 1
  83:    LET  fncg = 1 - x^4
  84: CASE 2
  85:    LET  fncg = 1 - x / 2
  86: CASE 3
  87:    LET  fncg = 1 - (1 - 2 * x)^4
  88: CASE 4
  89:    LET  fncg = 6 * x * (x - 1) / 5 + 1
  90: CASE 5
  91:    LET  fncg = (x ^2 + 2 * SQR(2)) / 4 
  92: CASE 6
  93:    LET  fncg = SQR(3) * (3 + 4 * x - 4 * x^2) / 8
  94: CASE 7
  95:    LET  fncg = 1 - 3 * (2 * x - 1)^2 / 5
  96: CASE 8
  97:    LET  fncg = SQR(3) * (4 - x^2) / 8
  98: CASE 9
  99:    LET  fncg = 2 * SQR(2) / 3 - 5 * (x - 1 / SQR(2))^2 / 4
 100: CASE 10
 101:    LET  fncg = 1 - x^3.68
 102: CASE 11
 103:    LET  fncg = 11 / 14 - 1 / 1178 / (40 * x * (x - 1) + 11)
 104: CASE 12
 105:    LET  fncg = 355 / 452 - 1 / 710000 / (30 * x * (16 * x - 17) + 141)
 106: END SELECT
 107: END FUNCTION
 108: 
 109: EXTERNAL FUNCTION S(FuncNo)
 110: SELECT CASE FuncNo
 111: CASE 1
 112:    LET  S = 4 / 5
 113: CASE 2
 114:    LET  S = 3 / 4
 115: CASE 3
 116:    LET  S = 4 / 5
 117: CASE 4
 118:    LET  S = 4 / 5
 119: CASE 5
 120:    LET  S = (6 * SQR(2) + 1) / 12
 121: CASE 6
 122:    LET  S = 11 * SQR(3) / 24
 123: CASE 7
 124:    LET  S = 4 / 5
 125: CASE 8
 126:    LET  S = 11 * SQR(3) / 24
 127: CASE 9
 128:    LET  S = (31 * SQR(2) - 25) / 24
 129: CASE 10
 130:    LET  S = 3.68 / 4.68
 131: CASE 11
 132:    LET  S = 11 / 14 - ATN(SQR(10)) / 1178 / SQR(10)
 133: CASE 12
 134:    LET  S = 355 / 452 - (ATN(75/SQR(295))+ATN(85/SQR(295))) / 2130000 / SQR(295)
 135: END SELECT
 136: END FUNCTION
 137: 

標本平均モンテカルロ法(加重サンプリングによる高精度化)

次に示す高精度化手法は、加重サンプリング(Importance sampling)と呼ばれています。ηを区間[0,1]で確率密度p(x)で分布する乱数とします。p(x)は確率なので、

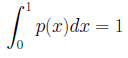
となることに注意します。次に、

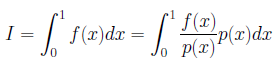
と変形しますと、期待値は、

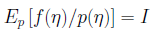
となります。E_pは、

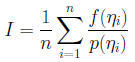
により計算できます。ここでp(x)は普通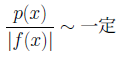となるように選びます。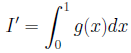だったので、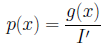とするとよいことが分かります。

このとき、

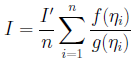
となります。なお、η_iは棄却法(rejection method)により生成できます。棄却法のフローチャートを次に示します。

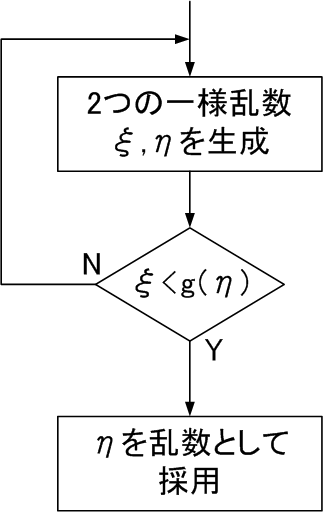
十進BASICのプログラムを次に示します。

PiSampleMean3.BAS

   1: !
   2: ! モンテカルロ法による円周率の計算
   3: ! 標本平均モンテカルロ法(加重サンプリングによる高精度化)
   4: !
   5: 
   6: ! 初期設定
   7: SET POINT STYLE 1
   8: SET WINDOW -0.2,1.2,-0.2,1.2
   9: DRAW grid
  10: RANDOMIZE
  11: 
  12: ! 外部定義関数の宣言
  13: DECLARE EXTERNAL FUNCTION fnc
  14: DECLARE EXTERNAL FUNCTION fncg
  15: DECLARE EXTERNAL FUNCTION S
  16: 
  17: ! 関数番号の入力
  18: INPUT PROMPT "関数番号(1..12)＝ " : FuncNo
  19: LET  FuncNo = INT(FuncNo)
  20: IF FuncNo < 1 THEN LET  FuncNo = 1
  21: IF FuncNo > 12 THEN LET  FuncNo = 12
  22: 
  23: ! 関数を描く
  24: FOR t = 0 TO 1 STEP 0.01
  25:    PLOT LINES: t, fnc(t, FuncNo);
  26: NEXT t
  27: PLOT LINES
  28: 
  29: INPUT PROMPT "試行回数＝ ": n
  30: LET sum = 0
  31: LET sumsq = 0
  32: FOR i = 1 TO n
  33: !確率密度分布がg(x)の乱数を発生させる
  34:    DO
  35:       LET x = RND
  36:    LOOP WHILE RND >= fncg(x, FuncNo)
  37:    LET y = fnc(x, FuncNo) / fncg(x, FuncNo) !yの値を計算する
  38:    LET sum = sum + y
  39:    SET LINE COLOR INT(RND * 8) !線の色をランダムに選ぶ
  40:    PLOT LINES :x,0;x,fnc(x, FuncNo)         !線を引く
  41: NEXT i
  42: 
  43: LET mean = sum / n
  44: 
  45: PRINT USING "円周率の推定値は ＝ %.##########":4 * mean * S(FuncNo)
  46: END
  47: 
  48: EXTERNAL FUNCTION fnc(x, FuncNo)
  49: SELECT CASE FuncNo
  50: CASE 1
  51:    LET  fnc = SQR(1 - x^2)
  52: CASE 2
  53:    LET  fnc = 1 / (1 + x^2)
  54: CASE 3
  55:    LET  fnc = 2 * SQR(x * (1 - x))
  56: CASE 4
  57:    LET  fnc = 1 / (x + SQR(1 - x^2))
  58: CASE 5
  59:    LET  fnc = 1 / SQR(2 - x^2) 
  60: CASE 6
  61:    LET  fnc = 3 * SQR(3) / 8 /(x^2 - x + 1)
  62: CASE 7
  63:    LET  fnc = 1 / 2 / (x^2 + (1 - x)^2)
  64: CASE 8
  65:    LET  fnc = 3 * SQR(3) / 2 / (3 + x^2)
  66: CASE 9
  67:    LET  fnc = SQR(2) / 3 / (x^2 - SQR(2)*x + 1)
  68: CASE 10
  69:    LET  fnc = 4 * (x - 1) / (x^4 - 2 * x^3 + 4 * x - 4)
  70: CASE 11
  71:    LET  fnc = 11 / 14 - x^4 * (1 - x)^4 / 4 / (1 + x^2)
  72: CASE 12
  73:    LET  fnc = 355 / 452 - x^8 * (1 - x)^8 * (25 + 816 * x^2) / 12656 / (1 + x^2)
  74: END SELECT
  75: END FUNCTION
  76: 
  77: EXTERNAL FUNCTION fncg(x, FuncNo)
  78: SELECT CASE FuncNo
  79: CASE 1
  80:    LET  fncg = 1 - x^4
  81: CASE 2
  82:    LET  fncg = 1 - x / 2
  83: CASE 3
  84:    LET  fncg = 1 - (1 - 2 * x)^4
  85: CASE 4
  86:    LET  fncg = 6 * x * (x - 1) / 5 + 1
  87: CASE 5
  88:    LET  fncg = (x ^2 + 2 * SQR(2)) / 4 
  89: CASE 6
  90:    LET  fncg = SQR(3) * (3 + 4 * x - 4 * x^2) / 8
  91: CASE 7
  92:    LET  fncg = 1 - 3 * (2 * x - 1)^2 / 5
  93: CASE 8
  94:    LET  fncg = SQR(3) * (4 - x^2) / 8
  95: CASE 9
  96:    LET  fncg = 2 * SQR(2) / 3 - 5 * (x - 1 / SQR(2))^2 / 4
  97: CASE 10
  98:    LET  fncg = 1 - x^3.68
  99: CASE 11
 100:    LET  fncg = 11 / 14 - 1 / 1178 / (40 * x * (x - 1) + 11)
 101: CASE 12
 102:    LET  fncg = 355 / 452 - 1 / 710000 / (30 * x * (16 * x - 17) + 141)
 103: END SELECT
 104: END FUNCTION
 105: 
 106: EXTERNAL FUNCTION S(FuncNo)
 107: SELECT CASE FuncNo
 108: CASE 1
 109:    LET  S = 4 / 5
 110: CASE 2
 111:    LET  S = 3 / 4
 112: CASE 3
 113:    LET  S = 4 / 5
 114: CASE 4
 115:    LET  S = 4 / 5
 116: CASE 5
 117:    LET  S = (6 * SQR(2) + 1) / 12
 118: CASE 6
 119:    LET  S = 11 * SQR(3) / 24
 120: CASE 7
 121:    LET  S = 4 / 5
 122: CASE 8
 123:    LET  S = 11 * SQR(3) / 24
 124: CASE 9
 125:    LET  S = (31 * SQR(2) - 25) / 24
 126: CASE 10
 127:    LET  S = 3.68 / 4.68
 128: CASE 11
 129:    LET  S = 11 / 14 - ATN(SQR(10)) / 1178 / SQR(10)
 130: CASE 12
 131:    LET  S = 355 / 452 - (ATN(75/SQR(295))+ATN(85/SQR(295))) / 2130000 / SQR(295)
 132: END SELECT
 133: END FUNCTION
 134: