円周率と連分数

連分数とその計算法

連分数によっても円周率を計算することができます。まず、連分数とはどのようなものか次に示します。いくつかの書き方で表すことができます。

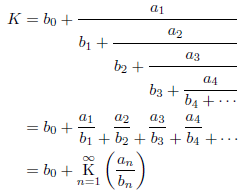
連分数の計算法は、次の2つが知られています。どちらも漸化式によります。

計算法その1

連分数Kの第n近似分数をとします。まず最初に、

とおきます。が確認できます。ついででは、

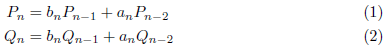
により、を次々と求めることができます。

計算法その2

参考文献[25]による方法です。式(1)において、両辺をP_n-1で割ると、

となります。ここで、とおくとであり、では、

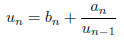
が得られます。同様にとおくとであり、では、

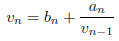
となります。計算法をまとめると、次のようになります。

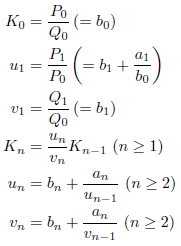
この方法では、先の方法と比べて桁あふれを起こしにくい特徴があります。しかし、b₀=0のときはうまく計算できません。そのときは、次のようにすればうまくいきます。

計算法その1

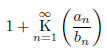を計算して、1を引きます。

計算法その2

求める連分数を、次のように変形します。とおいて、

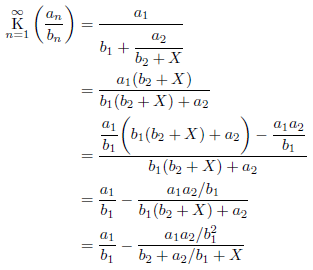
とします。すると、初期条件を

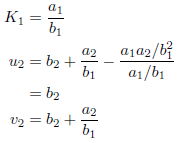
として、漸化式が計算できます。

例えば、Madhava-Gregory-Leibniz級数の収束の加速のページで述べた補正項の場合、次のように変形できます。

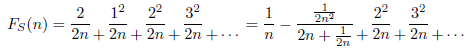
連分数と無限級数、無限乗積

無限級数、無限乗積は連分数に書き直すことができます。次に変換の方法を示します。

無限級数の連分数への変換

次の関係は、オイラーにより導かれました。

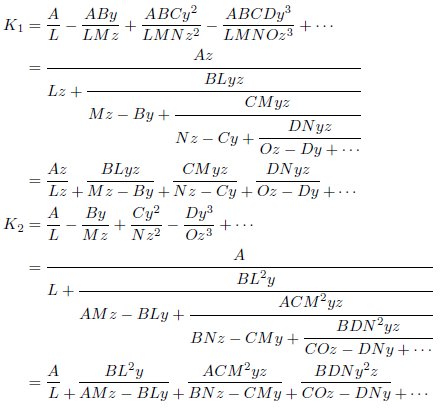
これより、次の関係式が導かれます。

また、という関係があるとき、

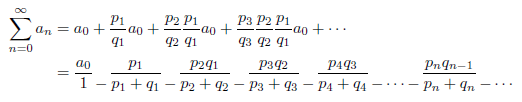
となります。

無限乗積の連分数への変換

次の変換が知られています。

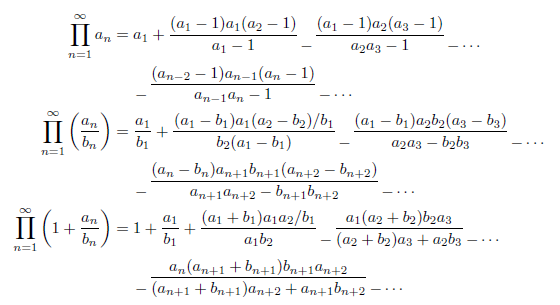
連分数の計算例

それでは、いくつかの例を挙げてみます。

例1：Wallis-Euler(ワリス－オイラー)

Wallisの無限乗積を次に示します。

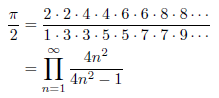
一方、次の連分数展開が知られています。

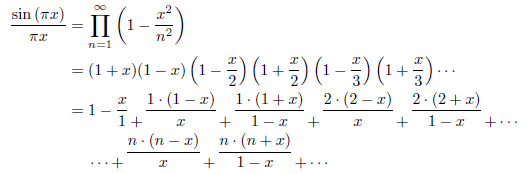
この式に、x=1/2を代入すると、連分数は次のようになります。Wallisの無限乗積と等価であることが分かります。

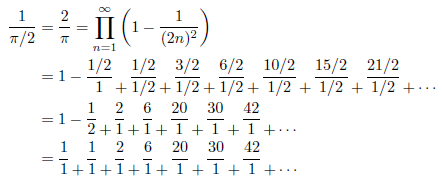
この連分数は、1739年にオイラーにより得られたとされます。

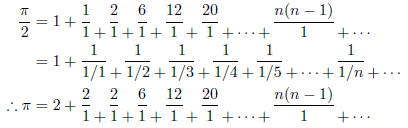
それでは、この連分数を計算してみることにします。まず、計算法その1により計算してみます。連分数の第n近似分数をとすると、円周率はにより求められます。漸化式は、初項を

として、では、

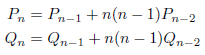
により求められます。十進BASICのプログラムを次に示します。

PiCFWallis1.BAS

   1: ! 十進1000桁モード
   2: OPTION ARITHMETIC DECIMAL_HIGH
   3: ! 繰り返し回数
   4: LET iter = 450
   5: 
   6: ! 初期値
   7: LET P0 = 2
   8: LET Q0 = 1
   9: PRINT USING "####":0;
  10: PRINT P0 / Q0
  11: LET P1 = 4
  12: LET Q1 = 1
  13: PRINT USING "####":1;
  14: PRINT P1 / Q1
  15: 
  16: ! 繰り返し
  17: FOR i = 2 TO iter
  18:    LET  P = P1 + i * (i - 1) * P0
  19:    LET  Q = Q1 + i * (i - 1) * Q0
  20:    PRINT USING "####":i;
  21:    PRINT P / Q
  22:    LET P0 = P1
  23:    LET Q0 = Q1
  24:    LET P1 = P
  25:    LET Q1 = Q
  26: NEXT i
  27: END

一方、計算法その2では、次のように計算できます。

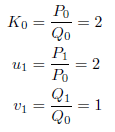
として、

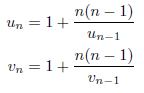
を計算すると、連分数の第n近似は、により求められます。十進BASICのプログラムを次に示します。

PiCFWallis2.BAS

   1: ! 十進1000桁モード
   2: OPTION ARITHMETIC DECIMAL_HIGH
   3: ! 繰り返し回数
   4: LET iter = 1000
   5: 
   6: ! 初期値
   7: LET K = 2
   8: PRINT USING "####":0;
   9: PRINT K
  10: LET u = 2
  11: LET v = 1
  12: LET K = u / v * K
  13: PRINT USING "####":1;
  14: PRINT K
  15: 
  16: ! 繰り返し
  17: FOR i = 2 TO iter
  18:    LET u = 1 + i * (i - 1) / u
  19:    LET v = 1 + i * (i - 1) / v
  20:    LET K = u / v * K
  21:    PRINT USING "####":i;
  22:    PRINT K
  23: NEXT i
  24: END

繰り返し回数は1000回としていますが、桁あふれを起こさないため、もっと大きく取れます。

ここで、計算法その1と、計算法その2を比較してみることにします。P_n、Q_nに比べてu_n、v_nが小さいため、桁あふれを起こしにくくなっています。またu_n、v_nの値は、Wallisの連分数の定義式に対応していることが理解できます。

n	P_n	Q_n	u_n	v_n	K_n
0	2	1			2.00000000
1	4	1	2	1	4.00000000
2	8	3	2	3	2.66666666
3	32	9	4	3	3.55555555
4	128	45	4	5	2.84444444
5	768	225	6	5	3.41333333
6	4608	1575	6	7	2.92571428
7	36864	11025	8	7	3.34367346
8	294912	99225	8	9	2.97215419
9	2949120	893025	10	9	3.30239355
10	29491200	9823275	10	11	3.00217595

例2：Brouncker-Gregory(ブラウンカー－グレゴリー)

Madhava-Gregory-Leibnizの無限級数を連分数に直すと次のようになります。

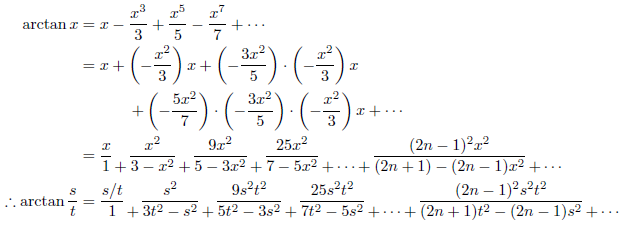
x=1を代入して、

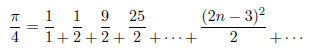
となります。この連分数はBrounckerの連分数と呼ばれ、歴史的にも重要です。

として、では、

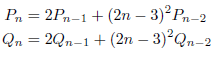
により求められます。十進BASICのプログラムを次に示します。

PiCFBrouncker1.BAS

   1: ! 十進1000桁モード
   2: OPTION ARITHMETIC DECIMAL_HIGH
   3: ! 繰り返し回数
   4: LET iter = 400
   5: 
   6: ! 初期値
   7: LET P0 = 0
   8: LET Q0 = 1
   9: PRINT USING "####":0;
  10: PRINT P0 / Q0
  11: LET P1 = 4
  12: LET Q1 = 1
  13: PRINT USING "####":1;
  14: PRINT P1 / Q1
  15: 
  16: ! 繰り返し
  17: FOR i = 2 TO iter
  18:    LET  P = 2 * P1 + (2 * i - 3)^2 * P0
  19:    LET  Q = 2 * Q1 + (2 * i - 3)^2 * Q0
  20:    PRINT USING "####":i;
  21:    PRINT P / Q
  22:    LET P0 = P1
  23:    LET Q0 = Q1
  24:    LET P1 = P
  25:    LET Q1 = Q
  26: NEXT i
  27: END

一方、計算法その2では、次のように計算できます。とから

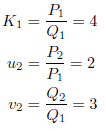
として、

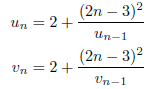
を計算すると、連分数の第n近似は、により求められます。十進BASICのプログラムを次に示します。

PiCFBrouncker2.BAS

   1: ! 十進1000桁モード
   2: OPTION ARITHMETIC DECIMAL_HIGH
   3: ! 繰り返し回数
   4: LET iter = 1000
   5: 
   6: ! 初期値
   7: LET K = 4
   8: PRINT USING "####":1;
   9: PRINT K
  10: LET u = 2
  11: LET v = 3
  12: LET K = u / v * K
  13: PRINT USING "####":2;
  14: PRINT K
  15: 
  16: ! 繰り返し
  17: FOR i = 3 TO iter
  18:    LET u = 2 + (2 * i - 3)^2 / u
  19:    LET v = 2 + (2 * i - 3)^2 / v
  20:    LET K = u / v * K
  21:    PRINT USING "####":i;
  22:    PRINT K
  23: NEXT i
  24: END

繰り返し回数は1000回としていますが、桁あふれを起こさないため、もっと大きく取れます。

例3：Ramanujan(ラマヌジャン)

次の無限級数は、インドの数学者ラマヌジャンにより、1914年に導かれました。

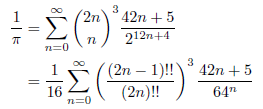
ここで、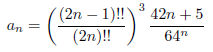とおくと漸化式は、

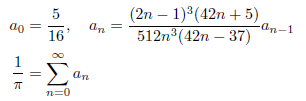
と表されます。したがって、とおくと、

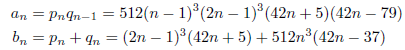
となることから、

となります。

として、では、

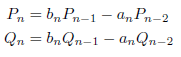
により求められます。十進BASICのプログラムを次に示します。

PiCFRamanujan1.BAS

   1: ! 十進1000桁モード
   2: OPTION ARITHMETIC DECIMAL_HIGH
   3: ! 繰り返し回数
   4: LET iter = 95
   5: 
   6: ! 初期値
   7: LET P0 = 16 / 5
   8: LET Q0 = 1
   9: PRINT USING "####":0;
  10: PRINT P0 / Q0
  11: LET P1 = 8192
  12: LET Q1 = 2607
  13: PRINT USING "####":1;
  14: PRINT P1 / Q1
  15: 
  16: ! 繰り返し
  17: FOR i = 2 TO iter
  18:    LET a = 512*(i-1)^3*(2*i-1)^3*(42*i+5)*(42*i-79)
  19:    LET b = (2*i-1)^3*(42*i+5)+512*i^3*(42*i-37)
  20:    LET  P = b * P1 - a * P0
  21:    LET  Q = b * Q1 - a * Q0
  22:    PRINT USING "####":i;
  23:    PRINT P / Q
  24:    LET P0 = P1
  25:    LET Q0 = Q1
  26:    LET P1 = P
  27:    LET Q1 = Q
  28: NEXT i
  29: END

一方、計算法その2では、次のように計算できます。

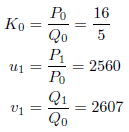
として、

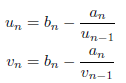
を計算すると、連分数の第n近似は、により求められます。十進BASICのプログラムを次に示します。

PiCFRamanujan2.BAS

   1: ! 十進1000桁モード
   2: OPTION ARITHMETIC DECIMAL_HIGH
   3: ! 繰り返し回数
   4: LET iter = 555
   5: 
   6: ! 初期値
   7: LET K = 16 / 5
   8: PRINT USING "####":0;
   9: PRINT K
  10: LET u = 2560
  11: LET v = 2607
  12: LET K = u / v * K
  13: PRINT USING "####":1;
  14: PRINT K
  15: 
  16: ! 繰り返し
  17: FOR i = 2 TO iter
  18:    LET a = 512*(i-1)^3*(2*i-1)^3*(42*i+5)*(42*i-79)
  19:    LET b = (2*i-1)^3*(42*i+5)+512*i^3*(42*i-37)
  20:    LET u = b - a / u
  21:    LET v = b - a / v
  22:    LET K = u / v * K
  23:    PRINT USING "####":i;
  24:    PRINT K
  25: NEXT i
  26: END

その他の話題(円周率の連分数に対する)

Madhava-Gregory-Leibniz級数の収束の加速のページで、次の補正項について言及しました。

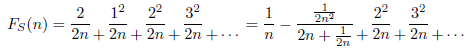
この補正項に関して、参考文献[46]には、次の式が証明されています。

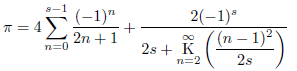
例えば、

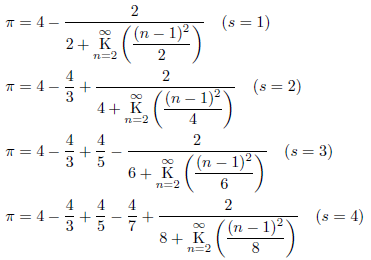
となります。一方、において、

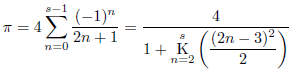
となることが知られています。よって、

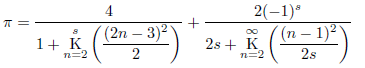
が成立します。