Madhava-Gregory-Leibniz級数の収束の加速(収束の加速1)

はじめに

円周率を与える無限級数のひとつにMadhava-Gregory-Leibniz級数があります。

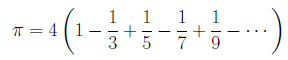
この無限級数は、収束が大変遅いことで知られています。古来より工夫されてきた、収束を速める手法について紹介いたします。

補正項(インドの数学を出発点にして)

15世紀、南インドの数学者たちは、補正項F_k(n)を用いてMadhava-Gregory-Leibniz級数の収束を速めることを考えました。

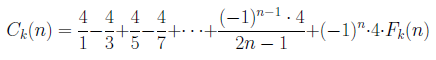
彼らは、試行錯誤の末、次の3つの補正項を導きました。

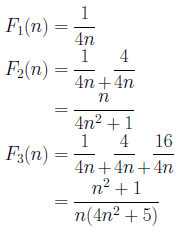
ところが補正項を次のように取ると、一般化できることが分かっています。補正項を

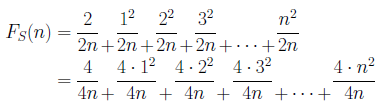
のようにとると、

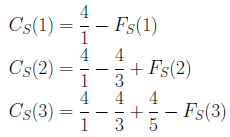
は、速く円周率に収束していきます。連分数の計算については、円周率と連分数のページを参照ください。

十進BASICでプログラムを書くと、次のようになります。十進1000桁モードで実行してみてください。

PiSugimoto.BAS

   1: OPTION BASE 1
   2: LET iter = 340
   3: DIM s(1 TO iter)
   4: !
   5: LET s(1) = 4
   6: LET f = -1
   7: FOR k = 2 TO iter
   8:    LET s(k) = s(k-1) + f * 4 / (2 * k - 1)
   9:    LET f = -f
  10: NEXT k
  11: 
  12: LET  f = -1
  13: FOR n = 1 TO iter
  14:    LET p1 = 0
  15:    LET q1 = 1
  16:    LET p2 = 2
  17:    LET q2 = 2 * n
  18:    FOR k = 1 TO n
  19:       LET p3 = 2 * n * p2 + k * k * p1
  20:       LET q3 = 2 * n * q2 + k * k * q1
  21:       LET p1 = p2
  22:       LET q1 = q2
  23:       LET p2 = p3
  24:       LET q2 = q3
  25:    NEXT k
  26:    PRINT USING "####":n;
  27:    PRINT s(n) + f * p3 / q3
  28:    LET f = -f
  29: NEXT n
  30: 
  31: END

ただし、このプログラムでは桁あふれのために、繰り返し数(変数iter)を340までしか取れません。そこで補正項の計算法を工夫して、桁あふれを回避してみました。十進1000桁モードで実行していただきたいのですが、除算が含まれるため、実行には時間がかかります。

PiSugimoto2.BAS

   1: OPTION BASE 1
   2: LET iter = 700
   3: DIM s(1 TO iter)
   4: !
   5: LET s(1) = 4
   6: LET f = -1
   7: FOR k = 2 TO iter
   8:    LET s(k) = s(k-1) + f * 4 / (2 * k - 1)
   9:    LET f = -f
  10: NEXT k
  11: 
  12: LET  f = -1
  13: FOR n = 1 TO iter
  14:    LET u = 2 * n + 2
  15:    LET v = 2 * n
  16:    LET D = 1 + 1 / n
  17:    FOR k = 1 TO n
  18:       LET u = 2 * n + k * k / u
  19:       LET v = 2 * n + k * k / v
  20:       LET D = u / v * D
  21:    NEXT k
  22:    PRINT USING "####":n;
  23:    PRINT s(n) + f * (D - 1)
  24:    LET f = -f
  25: NEXT n
  26: 
  27: END

Euler変換、AitkenのΔ²法など

交代級数の収束を速める手段として、Euler-Knopp変換(特にq=1のときEuler変換)があります。変換の式は、

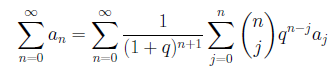
となります。実際の計算は、Wynnによるアルゴリズムが知られています。

十進BASICでプログラムを書くと、次のようになります。十進1000桁モードで実行してみてください。

PiEulerKnoppWynn.BAS

   1: OPTION BASE 0
   2: !
   3: LET iter = 300
   4: INPUT PROMPT "qの値 (オイラー変換の場合 q=1)":q
   5: DIM s(0 TO iter)
   6: !
   7: LET s(0) = 0
   8: LET f = 1
   9: FOR k = 1 TO iter
  10:    LET s(k) = s(k-1) + f * 4 / (2 * k - 1)
  11:    LET f = -f
  12: NEXT k
  13: 
  14: FOR j = 1 TO iter-1
  15:    FOR i = 0 TO iter-j
  16:       LET s(i) = (s(i + 1) + q * s(i)) / (1 + q)
  17:    NEXT i
  18:    PRINT USING "加速 #### 回目":j;
  19:    PRINT s(0)
  20: NEXT j
  21: 
  22: END

また、AitkenのΔ²法も、収束の加速法として知られています。変換の式は、

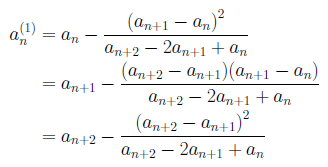
となります。この加速法は、繰り返し適用できます。

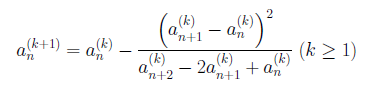
十進BASICでプログラムを書くと、次のようになります。十進1000桁モードで実行してみてください。

PiAitken.BAS

   1: OPTION BASE 0
   2: !
   3: LET iter = 300
   4: DIM s(0 TO iter-1)
   5: !
   6: LET s(0) = 4
   7: PRINT "   0    0  ";
   8: PRINT s(0)
   9: LET f = -1
  10: FOR i = 1 TO iter-1
  11:    LET s(i) = s(i-1) + f * 4 / (2 * i + 1)
  12:    LET f = -f
  13:    PRINT USING "   0 ####  ":i;
  14:    PRINT s(i)
  15: NEXT i
  16: 
  17: LET j = 1
  18: DO WHILE j <= (iter - 1) / 2
  19:    PRINT "=========================="
  20:    FOR i = 0 TO iter-2*j-1
  21:       LET s(i) = s(i) - (s(i+1) - s(i))^2 / (s(i+2) - 2*s(i+1) + s(i))
  22:       PRINT USING "#### ####  ":j,i;
  23:       PRINT s(i)
  24:    NEXT i
  25:    LET j = j + 1
  26: LOOP
  27: 
  28: END

sumalt法

PARIの開発者として有名なH.Cohenによるsumalt法も、交代級数の収束を加速させることで知られています。sumalt法のうち、Algorithm1は次のようになります。a_kは、加速したい交代級数のk番目の項です。最初のn項を足し合わせるとします。

このアルゴリズムのdは、

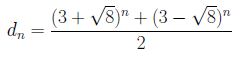
ですが、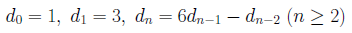によっても求めることができます。これは、Fibonacci数列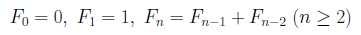に対するBinetの表示

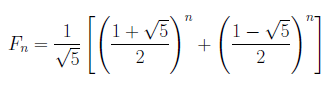
に相当します。一方、この数列の母関数は、

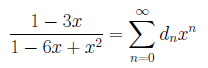
となります。Madhava-Gregory-Leibniz級数の場合の十進BASICのプログラムは、次のようになります。

PiSumalt1o.BAS

   1: OPTION BASE 0
   2: LET iter = 1300
   3: DIM t(0 TO iter-1)
   4: DIM d(0 TO iter)
   5: !
   6: FOR k = 0 TO iter-1
   7:    LET t(k) = 4 / (2 * k + 1)
   8: NEXT k
   9: 
  10: REM 係数の計算
  11: LET d(0) = 1
  12: LET d(1) = 3
  13: FOR k = 2 TO iter
  14:    LET d(k) = 6 * d(k - 1) - d(k - 2)
  15: NEXT k
  16: 
  17: REM 繰り返し計算
  18: FOR n = 1 TO iter
  19:    LET b = -1
  20:    LET c = -d(n)
  21:    LET s = 0
  22:    FOR k = 0 TO n-1
  23:       LET c = b - c
  24:       LET s = s + c * t(k)
  25:       LET b = b * 2 * (k + n) * (k - n) / (2 * k + 1) / (k + 1)
  26:    NEXT k
  27:    PRINT USING "####":n;
  28:    PRINT s / d(n)
  29: NEXT n
  30: END

また、次のようにも書けます。

PiSumalt1a.BAS

   1: OPTION BASE 0
   2: LET iter = 1300
   3: DIM t(0 TO iter-1)
   4: 
   5: REM
   6: LET f = 1
   7: FOR k = 0 TO iter-1
   8:    LET t(k) = f * 4 / (2 * k + 1)
   9:    LET f = -f
  10: NEXT k
  11: 
  12: REM 繰り返し計算
  13: FOR n = 1 TO iter
  14:    LET s = 0
  15:    LET b = 1
  16:    FOR k = 1 TO 2*n-1
  17:       LET b = 2 * b
  18:    NEXT k
  19:    LET  c = b
  20:    FOR k = n-1 TO 0 STEP -1
  21:       LET s = s + c * t(k)
  22:       LET b = b * (2 * k + 1) * (k + 1)/2/(n - k)/(n + k)
  23:       LET c = c + b
  24:    NEXT k
  25:    PRINT USING "####":n;
  26:    PRINT s / c
  27: next n
  28: END