はじめに
円周率の小数点以下d桁目を求めるためには、1,2,3,...,d-1桁目を計算しなければならないと考えられてきました。ところが1995年にSimon Plouffe(プラウフ)により発見された公式を用いると、円周率の16進数表示のd桁目をピンポイントに求められることが分かりました。この公式は、今日BBP(Bailey-Borwein-Plouffe)公式と呼ばれています。公式を次に示します。
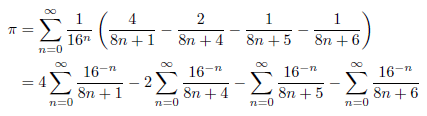
まず、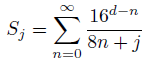 とおきます。xの小数部分を{x}としますと、円周率の小数点以下d+1桁目が知りたいときは、{16dπ}を求めればよいことが分かります。BBP公式を用いると、{16dπ}は、
とおきます。xの小数部分を{x}としますと、円周率の小数点以下d+1桁目が知りたいときは、{16dπ}を求めればよいことが分かります。BBP公式を用いると、{16dπ}は、
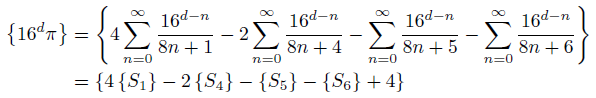
と表されます。最後に4を足しているのは、例えば、たまたま{S1}=0.00111、{S4}=0.98891、{S5}=0.89991、{S6}=0.90361、となったとき、本来4S1-2S4-S5-S6は正の数になるはずなのに、4{S1}-2{S4}-{S5}-{S6}は負になってしまうからです。ここで、{Sj}をもう少し詳しく見てみます。
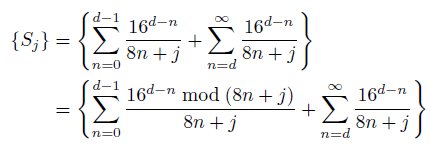
上の式において、第2項は1よりも小さいのですが、初項は1よりも大きくなってしまいます。ほしいのは小数部分なので、初項の分子を(8n+j)で割った余りを8n+jで割ることにします。円周率のd桁目を高速に求めるには、16d-n mod (8n+j)を効率よく求めなければなりません。
Binary Modulo Exponentiation
この節では、bk mod cの計算を考えます。bkの計算を行うには、次のf1(b,k)を計算すればよいことが分かります。
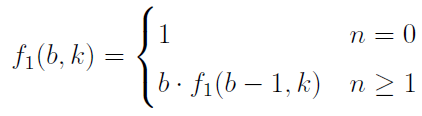
ところがf1(b,k)の計算は、特にkが大きい場合、計算に長時間を要します。そこで、次のf2(b,k)をみてみます。
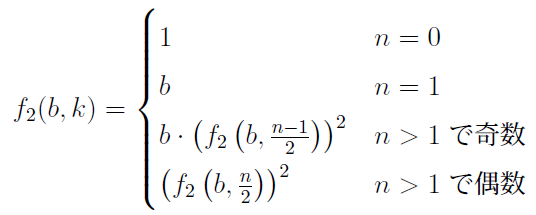
この関数で、例えばf2(b,23)を計算すると、次のようになります。
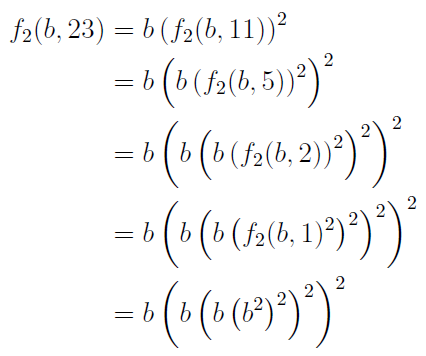
この計算では、bを"自乗して"、"自乗して"、"bをかけて"、"自乗して"、"bをかけて"、"自乗して"、"bをかける"、の7ステップで済むのですが、f1(b,23)の計算では、bを23回かけているので23ステップ必要です。kの値が大きくなればなるほど、f1(b,k)とf2(b,k)の計算に必要なステップ数は、かけ離れていきます。
f2(b,k)による計算を、Binary Modulo Exponeniationと称します。なぜBinaryというかと言いますと、例えばk=23の場合、23を二進数表示して10111としたとき、0をS、1をSBと置き換えて、SBSSBSBSBという文字列を得、最初のSBを除きSSBSBSBとして、Sを"自乗して"、Bを"bをかけて"と呼ぶと、先に挙げたf2(b,23)の計算と同じになるからです。
Binary Modulo Exponentiationは、2000年以上前のインドですでに知られていたということです。Binary Modulo Exponentiationを利用してr=bk mod cを求めるためのアルゴリズムは、次のようになります。
r := b mod c;
t := (the greatest power of 2 that is not bigger than k);
k := k - t;
while (t > 1)
{
t := t / 2;
r := r^2 mod c;
if (k >= t)
{
k := k - t;
r := b・r mod c;
}
}
ここまでくると、プログラムできます。
BBPアルゴリズムのプログラム
十進BASICによるプログラムを次に示します。10進数でdを入力すると小数点以下d桁目からd+7桁目までを16進数で表示します。dは、1から229まで可能ですが、大きい桁数を求めようとすると長い時間がかかりますので、ご注意ください。
BBP.BAS
1: ! 2: ! BBP algorithm 3: ! 4: ! This program computes the p-th hexadecimal digit of pi 5: ! (plus the following 7 digits) 6: ! 7: ! Input 8: ! d (1 <= d <= 2^29) 9: ! d = 1 means the first digit after the radix point 10: ! 11: 12: OPTION ARITHMETIC DECIMAL 13: DECLARE EXTERNAL FUNCTION BinModExp 14: DECLARE EXTERNAL FUNCTION SumOfTerms 15: 16: LET Dmax = 2^29 17: INPUT PROMPT "d = ":d 18: IF d < 1 THEN LET d = 1 19: IF d > Dmax THEN LET d = Dmax 20: 21: LET s = 4 * SumOfTerms(8, 1, d-1) 22: LET s = s - 2 * SumOfTerms(8, 4, d-1) 23: LET s = s - SumOfTerms(8, 5, d-1) 24: LET s = s - SumOfTerms(8, 6, d-1) 25: PRINT BSTR$(INT(MOD(s + 4, 1) * 2^32), 16) ! 16^8 = 2^32 26: END 27: 28: ! Binary modulo exponentiation 29: ! 30: ! r = b^k mod c 31: ! 32: EXTERNAL FUNCTION BinModExp(b, k, c) 33: OPTION ARITHMETIC DECIMAL 34: 35: IF c = 1 THEN 36: LET BinModExp = 0 37: ELSEIF k = 0 THEN 38: LET BinModExp = 1 39: ELSEIF k = 1 THEN 40: LET BinModExp = MOD(b, c) 41: ELSE 42: LET r = MOD(b, c) 43: LET t = 1 44: DO WHILE t <= k 45: LET t = t * 2 46: LOOP 47: LET t = t / 2 48: 49: LET k = k - t 50: DO WHILE t > 1 51: LET t = t / 2 52: LET r = MOD(r * r, c) 53: IF k >= t THEN 54: LET k = k - t 55: LET r = MOD(b * r, c) 56: END IF 57: LOOP 58: LET BinModExp = r 59: END IF 60: END FUNCTION 61: 62: ! 63: ! This function computes the fractional part of 64: ! 65: ! sum_n (16^(d - n) mod (j * n + m) / (j * n + m)) 66: ! n = 0, 1, 2,..., d-1 67: ! + sum_n (16^(d - n) / (j * n + m)) 68: ! n = d, d+1, d+2,... 69: ! 70: EXTERNAL FUNCTION SumOfTerms(j, m, d) 71: OPTION ARITHMETIC DECIMAL 72: LET s = 0 73: 74: ! sum of terms n = 0, 1, 2,..., d-1 75: FOR n = 0 TO d-1 76: LET x = BinModExp(16, d - n, m) 77: LET s = s + x / m 78: LET s = MOD(s, 1) 79: LET m = m + j 80: NEXT n 81: 82: ! sum of terms n = d, d+1, d+2,... 83: ! some additional terms for 8 hex digit accurracy 84: LET epsT = 16^(-10) / 4 85: 86: LET t = 1 ! t = 16^(d - d) 87: LET x = t / m 88: DO 89: LET s = s + x 90: LET t = t / 16 91: LET m = m + j 92: LET x = t / m 93: LOOP WHILE x > epsT 94: 95: LET SumOfTerms = s 96: END FUNCTION
円周率の16進数表示
円周率の16進数表示は、10進数表示ほど知られておりません。そこで、十進BASICによるプログラムを示します。十進1000桁モードで得られる円周率の値をもとにすると、16進数で829桁の値が得られます。
PiHex.BAS
1: ! 2: ! 円周率の16進数表示 3: ! 4: OPTION ARITHMETIC DECIMAL_HIGH 5: 6: ! 整数部 7: LET p = PI 8: LET h = INT(p) 9: PRINT " ";BSTR$(h,16);"." 10: LET p = p - h 11: 12: ! 小数部 13: FOR d = 1 TO 829 14: IF MOD(d, 50) = 1 THEN PRINT USING "(%%%%): ":d; 15: LET p = p * 16 16: LET h = INT(p) 17: PRINT BSTR$(h, 16); 18: LET p = p - h 19: IF MOD(d, 50) = 0 THEN 20: PRINT 21: ELSEIF MOD(d, 10) = 0 THEN 22: PRINT " "; 23: END IF 24: NEXT d 25: END
BBP公式の証明
次にBBP公式の証明を示します。任意の自然数kに対して、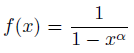 のマクローリン展開が、
のマクローリン展開が、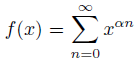 となることを用いると
となることを用いると
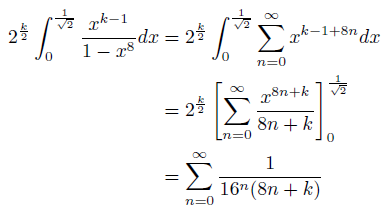
が成り立ちます。よって、k=1,4,5,6の場合を考えますと、
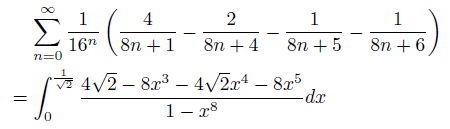
となります。ここで、![]() と変数変換しますと、
と変数変換しますと、
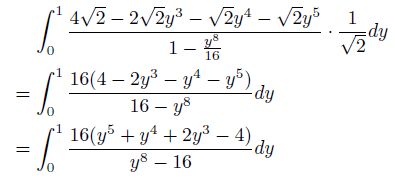
となりますが、ここで
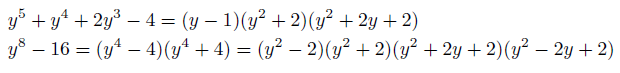
と因数分解できることに注意しますと、上の積分は、
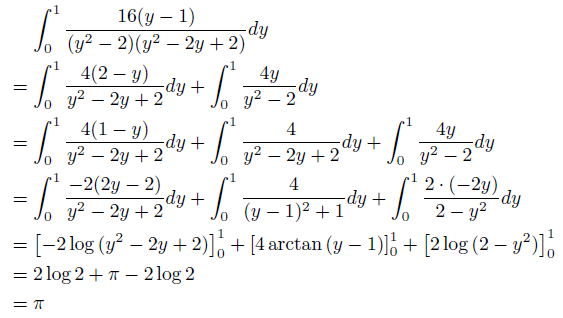
となり、BBP公式が証明されました。
その他のBBP型公式の例
まず、次の因数分解から出発します。
![]()
したがって、
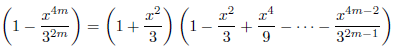
となります。また、![]() のとき、
のとき、
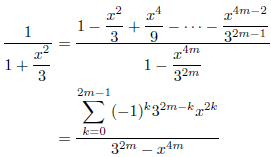
が成立します。一方、
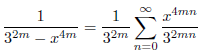
なので、
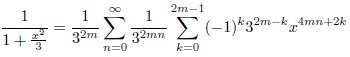
となります。ここで、
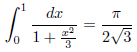
なので、
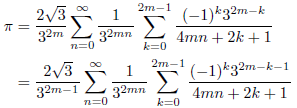
となります。したがって、
m=1のとき
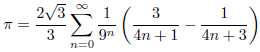
m=2のとき
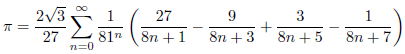
m=3のとき
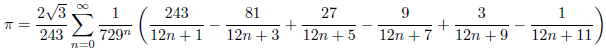
m=4のとき