円周率と繰り返し計算

はじめに

以下の公式を用いて計算する場合、乗算をFFTを用いて高速化する等のテクニックがしばしば用いられますが、1000桁程度では特別なテクニックを使わなくても充分高速です。

アルキメデスの公式

アルキメデスは、単位円に内接・外接する正多角形から円周率の値を計算しました。正96角形までの結果より、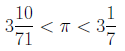を得ました。

現代の書き方で漸化式を書くと、次のようになります。内接正ｎ角形の半周の長さをｌ_n、外接正ｎ角形の半周の長さをL_nで表すと、次の関係式が得られます。

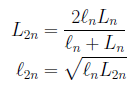
十進BASICでプログラムを書くと、次のようになります。十進1000桁モードで実行してみてください。

PiArchimedes.BAS

   1: ! 繰り返し回数
   2: LET iter = 1700
   3: 
   4: ! 初期値
   5: LET a = 2 * SQR(2)
   6: LET b = 4
   7: 
   8: ! 繰り返し
   9: FOR i = 1 TO iter
  10:    LET b = 2 * a * b / (a + b)
  11:    LET a = SQR(a * b)
  12:    PRINT USING "####": i;
  13:    PRINT a
  14: NEXT i
  15: END

Salamin、Brentの公式

1809年、Gaussは円周率と算術幾何平均に関係があることを発見しました。1976年にSalaminとBrentはこの関係に再注目し、円周率が高速に求められることを示しました。さらに、SchoenhageとStrassenは乗算を減らす巧みな方法を見出しました。以下にこのアルゴリズムを示します。

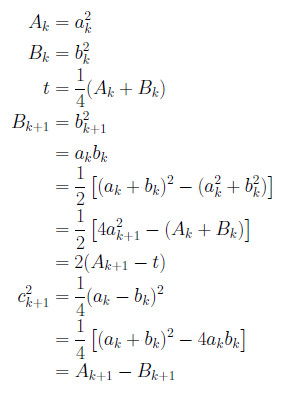
十進BASICでプログラムを書くと、次のようになります。十進1000桁モードで実行してみてください。

PiGaussSalaminBrent.BAS

   1: ! 繰り返し回数
   2: LET iter = 11
   3: 
   4: ! 初期値
   5: LET a = 1
   6: LET aa = 1
   7: LET b = 0.5
   8: LET s = 0.5
   9: LET c = 1
  10: 
  11: ! 繰り返し
  12: FOR i = 1 TO iter
  13:    LET t = (aa + b) / 4
  14:    LET b = SQR(b)
  15:    LET a = (a + b) / 2
  16:    LET aa = a * a
  17:    LET b = 2 * (aa - t)
  18:    LET c = 2 * c
  19:    LET s = s + c * (b - aa)
  20:    PRINT USING "###" : i;
  21:    PRINT (aa + b) / s
  22: NEXT i
  23: END

Borwein兄弟の公式

次に示す公式のa_kは1/πに4次収束することが知られています。

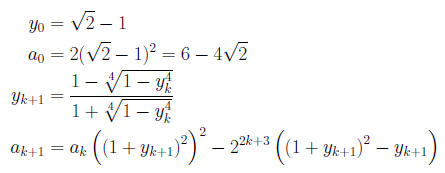
十進BASICでプログラムを書くと、次のようになります。十進1000桁モードで実行してみてください。

PiBorwein.BAS

   1: ! 繰り返し回数
   2: LET iter = 6
   3: 
   4: ! 初期値
   5: LET y = SQR(2) - 1
   6: LET a = 2 * y * y
   7: LET c = 2
   8: 
   9: ! 繰り返し
  10: FOR i = 1 TO iter
  11:    LET t = SQR(SQR(1 - y * y * y * y))
  12:    LET y = (1 - t) / (1 + t)
  13:    LET b = (1 + y) * (1 + y)
  14:    LET c = 4 * c
  15:    LET a = a * b * b - c * y * (b - y)
  16:    PRINT USING "###": i;
  17:    PRINT 1 / a
  18: NEXT i
  19: END