はじめに
L-systemはA. Lindenmayerにちなんで名づけられたシステムで、青緑色のバクテリアAnabaena catenulaや多くの藻類の細胞分裂のモデルとして提唱されました。今Aを通常の細胞、Bを未熟な細胞とします。Aは分裂してAとBに(A→AB)、Bは生長してAになる(B→A)とします。1つの未熟な細胞Bが、どのように生長するか示します。
| ステップ | 細胞の並び | 文字数 |
|---|---|---|
| 0 | B | 1 |
| 1 | A | 1 |
| 2 | AB | 2 |
| 3 | ABA | 3 |
| 4 | ABAAB | 5 |
| 5 | ABAABABA | 8 |
このようにして得られたAとBからなる文字列が、藻類の細胞の並びをよくシミュレートしています。これを、文字列の書き換え規則と捕らえると、容易にプログラミングできます。ちなみに、表中の文字数はFibonacci 数になっています。
このホームページでは
下記に示す基本的なルールのみでどこまで描けるか試みましたので、ご覧ください。
| 記号 | 意味 |
|---|---|
| Fまたはf | 線を描いて進む |
| Gまたはg | 線を描かずに進む |
| F、G以外のアルファベット | 進まない |
| + | 指定の角度だけ時計回りに向く |
| - | 指定の角度だけ反時計回りに向く |
| 自然数n | 角度+または-をn倍する(+++を3+) |
| [ | 位置と向きをスタックに保存する |
| ] | 位置と向きをスタックから呼び出す |
以後、記号の意味を説明します。
例1 (Fと+、-)
書き換え規則をF→F-F++F-Fとしたとき、最初の文字列をFとすると、次の文字列が得られます。
| ステップ | 文字列 |
|---|---|
| 0 | F |
| 1 | F-F++F-F |
| 2 | F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F |
| 3 | F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F-F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F-F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F |
ここで、Fを一歩前に進む、+を時計回りに指定された角度(例えば60度)曲がる、-を反時計回りに指定された角度曲がる、としますとグラフィカルに結果を把握することができるようになります。次に図を示します。Koch曲線としてよく知られている曲線が得られます。
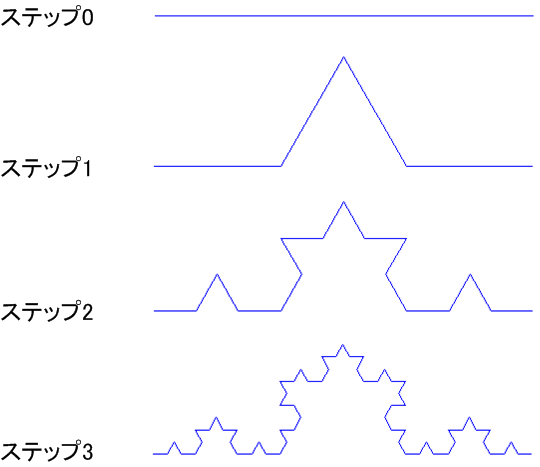
例2 (G)
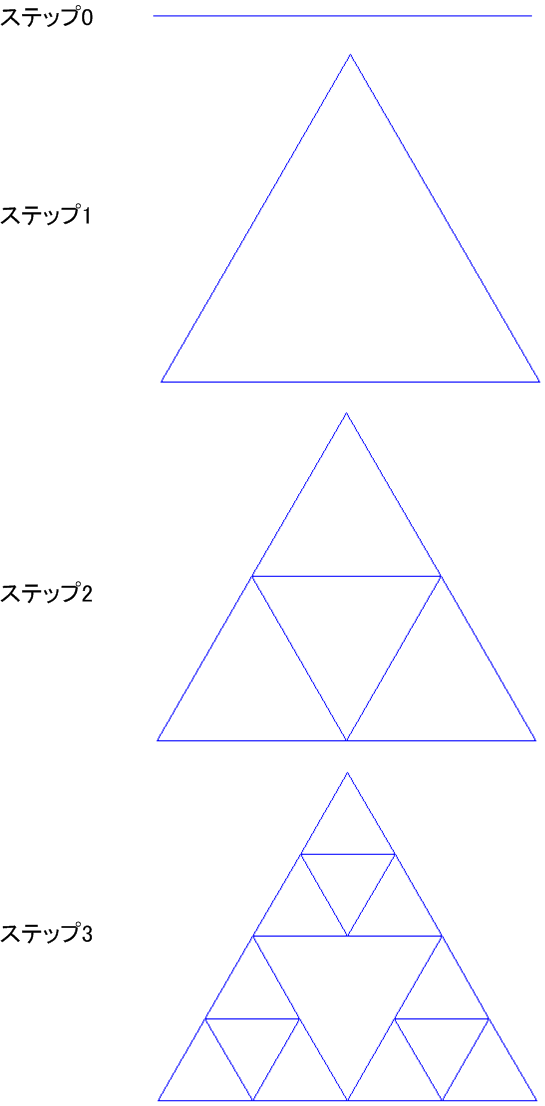
次に、アルファベットのGを紹介します。GもFと同様に一歩前に進むのですが、Fと異なり線を描かずに進みます。書き換え規則を、F→F-F-F-GG、G→GGとします。-を反時計回りの120度回転とするとき、文字列Fから出発すると、次のようになります。Sierpinskiのガスケットと呼ばれる図形です。
| ステップ | 文字列 |
|---|---|
| 0 | F |
| 1 | F-F-F-GG |
| 2 | F-F-F-GG-F-F-F-GG-F-F-F-GG-GGGG |
| 3 | F-F-F-GG-F-F-F-GG-F-F-F-GG-GGGG-F-F-F-GG-F-F-F-GG-F-F-F-GG-GGGG-F-F-F-GG-F-F-F-GG-F-F-F-GG-GGGG-GGGGGGGG |
例3 (F、G以外のアルファベット)
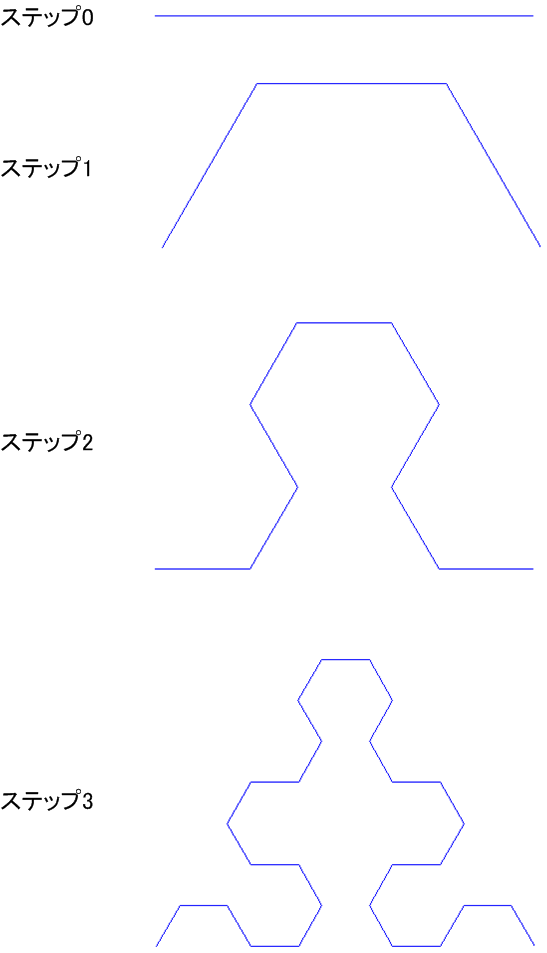
FとG以外のアルファベットは、線も描かなければ、ステップを進めることもしません。次の例は、書き換え規則を、L→-RF+LF+RF-、R→+LF-RF-LF+、F→とした場合です。ここでF→とは、アルファベットFを削除することを示します。出発する文字列をLFとしたときのステップ0からステップ1への変換は、まずLFをLに変換し(F→を適用)、ついでLを-RF+LF+RF-に変換(L→-RF+LF+RF-を適用)すると考えるとわかりやすいかもしれません。この規則により得られるのは、Sierpinski Arrowheadと呼ばれる図形で、ステップを進めるとSierpinskiのガスケットになります。
| ステップ | 文字列 |
|---|---|
| 0 | LF |
| 1 | -RF+LF+RF- |
| 2 | -+LF-RF-LF++-RF+LF+RF-++LF-RF-LF+- |
| 3 | -+-RF+LF+RF--+LF-RF-LF+--RF+LF+RF-++-+LF-RF-LF++-RF+LF+RF-++LF-RF-LF+-++-RF+LF+RF--+LF-RF-LF+--RF+LF+RF-+- |
例4 ( [ と ] )
最後に、記号 [ と ] を説明します。[ に遭遇すると、現時点の位置と方向を覚えておきます(スタックにいれます)。ついで[ から ] までを先に描いてから、さっき記憶したところから再スタートします。次の例は、書き換え規則をF→F[+F-F-F]F[--F+F+F]としたときの例です。文字列Fから角度15度で描くと、次の図が得られます。植物を思わせる図を、簡単な規則で描けることが理解いただけたかと思います。
| ステップ | 文字列 |
|---|---|
| 0 | F |
| 1 | F[+F-F-F]F[--F+F+F] |
| 2 | F[+F-F-F]F[--F+F+F][+F[+F-F-F]F[--F+F+F]-F[+F-F-F]F[--F+F+F]-F[+F-F-F]F[--F+F+F]]F[+F-F-F]F[--F+F+F][--F[+F-F-F]F[--F+F+F]+F[+F-F-F]F[--F+F+F]+F[+F-F-F]F[--F+F+F]] |
| 3 | F[+F-F-F]F[--F+F+F][+F[+F-F-F]F[--F+F+F]-F[+F-F-F]F[--F+F+F]-F[+F-F-F]F[--F+F+F]]F[+F-F-F]F[--F+F+F][--F[+F-F-F]F[--F+F+F]+F[+F-F-F]F[--F+F+F]+F[+F-F-F]F[--F+F+F]][+F[+F-F-F]F[--F+F+F][+F[+F-F-F]F[--F+F+F]-F[+F-F-F]F[--F+F+F]-F[+F-F-F]F[--F+F+F]]F[+F-F-F]F[--F+F+F][--F[+F-F-F]F[--F+F+F]+F[+F-F-F]F[--F+F+F]+F[+F-F-F]F[--F+F+F]]-F[+F-F-F]F[--F+F+F][+F[+F-F-F]F[--F+F+F]-F[+F-F-F]F[--F+F+F]-F[+F-F-F]F[--F+F+F]]F[+F-F-F]F[--F+F+F][--F[+F-F-F]F[--F+F+F]+F[+F-F-F]F[--F+F+F]+F[+F-F-F]F[--F+F+F]]-F[+F-F-F]F[--F+F+F][+F[+F-F-F]F[--F+F+F]-F[+F-F-F]F[--F+F+F]-F[+F-F-F]F[--F+F+F]]F[+F-F-F]F[--F+F+F][--F[+F-F-F]F[--F+F+F]+F[+F-F-F]F[--F+F+F]+F[+F-F-F]F[--F+F+F]]]F[+F-F-F]F[--F+F+F][+F[+F-F-F]F[--F+F+F]-F[+F-F-F]F[--F+F+F]-F[+F-F-F]F[--F+F+F]]F[+F-F-F]F[--F+F+F][--F[+F-F-F]F[--F+F+F]+F[+F-F-F]F[--F+F+F]+F[+F-F-F]F[--F+F+F]][--F[+F-F-F]F[--F+F+F][+F[+F-F-F]F[--F+F+F]-F[+F-F-F]F[--F+F+F]-F[+F-F-F]F[--F+F+F]]F[+F-F-F]F[--F+F+F][--F[+F-F-F]F[--F+F+F]+F[+F-F-F]F[--F+F+F]+F[+F-F-F]F[--F+F+F]]+F[+F-F-F]F[--F+F+F][+F[+F-F-F]F[--F+F+F]-F[+F-F-F]F[--F+F+F]-F[+F-F-F]F[--F+F+F]]F[+F-F-F]F[--F+F+F][--F[+F-F-F]F[--F+F+F]+F[+F-F-F]F[--F+F+F]+F[+F-F-F]F[--F+F+F]]+F[+F-F-F]F[--F+F+F][+F[+F-F-F]F[--F+F+F]-F[+F-F-F]F[--F+F+F]-F[+F-F-F]F[--F+F+F]]F[+F-F-F]F[--F+F+F][--F[+F-F-F]F[--F+F+F]+F[+F-F-F]F[--F+F+F]+F[+F-F-F]F[--F+F+F]]] |

ソフトウェア
L-systemにより図を描いてみたい方々のために、簡単なソフトウェア(Lsys2J)を用意いたしました。現在のところ、Windows版しかありませんが、ご利用ください。インストールは、レジストリを使っておりませんので、解凍していただくだけで結構です。アンインストールも、ファイルを削除していただくだけです。
参考文献
- P.Prusinkiewicz, A.Lindenmayer, The Algorithmic Beauty of Plants, Springer-Verlag, ISBN 0-387-97297-8
- P.Prusinkiewicz, J.Hanan, Lindenmayer Systems, Fractals, and Plants, Springer-Verlag, ISBN 3-540-97092-4
- G.W.Flake , The Computational Beauty of Nature: Computer Explorations of Fractals, Chaos, Complex Systems, and Adaptation, The MIT Press, ISBN 0-262-56127-1
- R.T.Stevens, Fractal Programming in Turbo Pascal, M&T Publishing Inc., ISBN 1-55851-106-7
- R.T.Stevens, Understanding Self-similar Fractals, R&T Technical Books, ISBN 0-13-436676-X
- R.T.Stevens, Creating Fractals , Charles River Media, ISBN 1-58450-423-4
- F.Drewes, Grammatical Picture Generation, Springer-Verlag, 3-540-21304-X
- J.Mishra, S.Mishra, L-System Fractals, Elsevier, ISBN 0-444-52832-6-431-70775-1
- J. Akiyama, H. Fukuda, H. Ito, and G. Nakamura, Infinite Series of Generalized Gosper Space Filling Curves, Lecture Notes in Computer Science 4381, Discrete Geometry, Combinatorics and Graph Theory, CJCDGCGT 2005, 1--9 (Springer, 2007).
- H.ザーガン、空間充填曲線とフラクタル、シュプリンガーフェアラーク東京, ISBN 4-431-70775-1
- パイトゲン、ザウペ、フラクタルイメージ 理論とプログラミング、シュプリンガーフェアラーク東京, ISBN 4-431-70569-4
- http://spanky.triumf.ca/pub/fractals/lsystems/
- http://www.seanet.com/~garyteachout/fill.html