はじめに
無限級数をもとに円周率を計算するとき、各項の数値を足し合わせていかなければなりません。このとき、初項から順に足し合わせていくと、長時間を要する場合があります。特に除算を含む項の計算は、求めようとする桁数が大きい場合、計算時間に大きな影響を及ぼします。
このような場合に大きな威力を発揮するのがBinary Splitting法です。この方法では、項の総和を順に計算するのではなく、トーナメント方式で足し合わせていきます。足す順序の変更に加え、除算の回数を減らす工夫がなされているために、計算時間が短くなります。東京大学の金田研究室による1兆2411億桁の円周率計算にも用いられたことでよく知られています。
ここではChudnovskyの無限級数と高野の公式を例に、説明をしてみたいと思います。足し合わせる項の数Lが2nに等しい場合は、非再帰的にコーディングすることができます。一方、Lが2nと異なる場合には、再帰的にコーディングする必要があります。注意していただきたいのは、1000桁の計算をするためには、計算の途中で1000桁以上の数値を必要とします。そのため、最終的に得られる数値の精度は、1000桁より少なくなります。
アルゴリズム(L=2nのとき)
L=2nであるとします。SLを、計算したい無限級数の第0項から第L-1項までの部分和とするとき、次の形の級数展開を考えます。
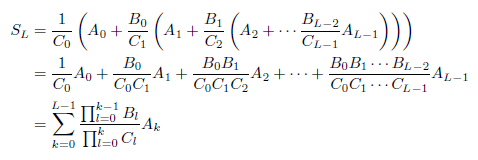
ここで、隣り合った項を足してみます。次のようになります。
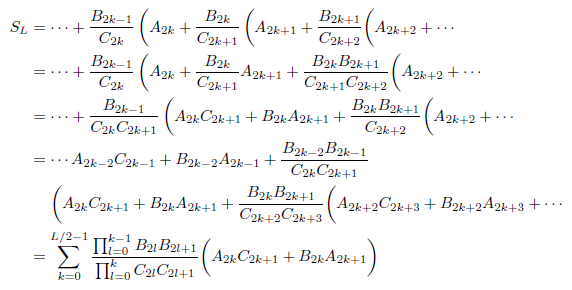
得られた結果は最初に示したSLと形式的に同じで、項の数が半分、すなわち2n-1に減っています。したがって、同様の計算を繰り返すたびに、項の数は半分になります。もう少しプログラミングしやすい形に書き直してみますと、
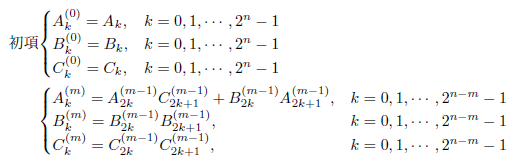
となります。計算をm=0...nと繰り返しますと、A0(n)/C0(n)がSLに等しくなります。もし、もとの級数が円周率の逆数だったときは、C0(n)/A0(n)を計算すればよいことになります。いずれの場合でも、除算は最後の1回のみでよいことに注意してください。
アルゴリズム(Lが2nでないとき)
一方、Lが2nでないとき、項の数は半分、半分にしていくわけにはいきません。そこで、半分ではなく、
LET mid = INT((n0 + n1) / 2)
で項を区切ります。再帰的に区切りを進めていき、隣り合った項まで区切られたときに、それらの項をまとめる方式をとります。
Chudnovskyの無限級数
ここで計算する無限級数は、Chudnovsky(チュドノフスキー)兄弟により見出されました。この無限級数は、1996年に、当時の世界記録80億桁の計算に用いられたことで有名です。
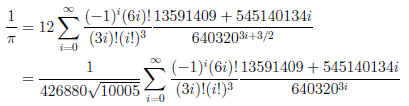
この式から、Binary Splitting法の計算に必要なAi、Bi、Ciは、次のようになります。
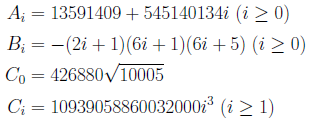
再帰版のプログラムでは、この定義でコーディングしますが、非再帰版のプログラムでは、まず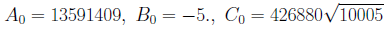 として、ついでi=1...L-1まで
として、ついでi=1...L-1まで
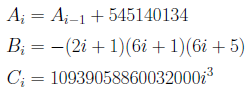
とします。最初に非再帰版の十進BASICのプログラムを示します。足し合わせる項の数L=2^5で小数点以下456桁の精度があります。
PiChudnovsky.BAS
1: ! Chudnovskyの公式による円周率の計算 2: ! 非再帰版 Binary splitting 3: OPTION BASE 0 4: OPTION ARITHMETIC decimal_high 5: 6: ! 足し合わせる項の数 7: LET L = 2^5 ! 足し合わせる項の数は2^nの形 8: 9: DIM A(0 TO L-1) 10: DIM B(0 TO L-1) 11: DIM C(0 TO L-1) 12: 13: ! 配列 A(), B(), C() のセット 14: LET A(0) = 13591409 15: LET B(0) = -5 16: LET C(0) = 426880 * SQR(10005) 17: FOR i = 1 TO L-1 18: LET A(i) = A(i-1) + 545140134 19: LET B(i) = -(2 * i + 1) * (6 * i + 1) * (6 * i + 5) 20: LET C(i) = 10939058860032000 * i^3 21: NEXT i 22: 23: ! 繰り返し計算 24: LET n = L / 2 25: DO WHILE n >= 1 26: FOR i = 0 TO n-1 27: LET A(i) = A(2 * i) * C(2 * i + 1) + B(2 * i) * A(2 * i + 1) 28: LET B(i) = B(2 * i) * B(2 * i + 1) 29: LET C(i) = C(2 * i) * C(2 * i + 1) 30: NEXT i 31: LET n = n / 2 32: LOOP 33: ! 結果の出力 34: PRINT C(0) / A(0) 35: 36: END
次に、再帰版の十進BASICのプログラムを示します。足し合わせる項の数L=51で小数点以下726桁の精度があります。
PiChudnovskyR.BAS
1: ! Chudnovskyの公式による円周率の計算 2: ! 再帰版 Binary splitting 3: OPTION ARITHMETIC decimal_high 4: DECLARE EXTERNAL SUB RecursiveAtnR 5: DIM X(1 TO 3) 6: LET A = 1 7: LET B = 2 8: LET C = 3 9: LET X(A) = 0 10: LET X(B) = 0 11: LET X(C) = 0 12: 13: LET L = 51 ! 足し合わせる項の数は2^nの形でなくてもよい 14: CALL RecursiveAtnR(0, L, X) 15: PRINT X(C) / X(A) 16: !PRINT X(C) / X(A) - PI 17: 18: END 19: 20: EXTERNAL SUB RecursiveAtnR(n0, n1, Q()) 21: OPTION ARITHMETIC decimal_high 22: DIM left(1 TO 3) 23: DIM right(1 TO 3) 24: 25: LET A = 1 26: LET B = 2 27: LET C = 3 28: 29: LET left(A) = 0 30: LET left(B) = 0 31: LET left(C) = 0 32: LET right(A) = 0 33: LET right(B) = 0 34: LET right(C) = 0 35: 36: IF n1 - n0 = 1 THEN 37: LET Q(A) = 13591409 + 545140134 * n0 38: LET Q(B) = -(2 * n0 + 1) * (6 * n0 + 1) * (6 * n0 + 5) 39: LET Q(C) = 10939058860032000 * n0^3 40: IF n0 = 0 THEN 41: LET Q(C) = 426880 * SQR(10005) 42: END IF 43: EXIT SUB 44: END IF 45: 46: LET mid = INT((n0 + n1) / 2) 47: 48: CALL RecursiveAtnR(n0, mid, left) 49: CALL RecursiveAtnR(mid, n1, right) 50: 51: LET Q(A) = left(A) * right(C) + left(B) * right(A) 52: LET Q(B) = left(B) * right(B) 53: LET Q(C) = left(C) * right(C) 54: 55: END SUB
高野の公式
高野の公式は、2002年に1兆2411億桁の計算で使われた公式で、2008年7月現在でも、世界記録を保持しています。無限級数は、次の形をしています。
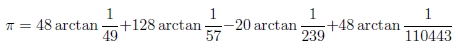
この式を用いて計算するためには、逆正接関数(arctan、十進BASICではATN)を計算しなければなりません。arctanの無限級数展開には、次の2つが知られています。
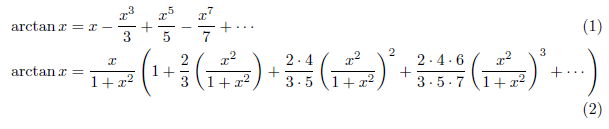
式(1)はMadhava-Gregory-Leibniz級数と呼ばれ、式(2)はEulerにより求められました。2つの式は見た目がずいぶん異なりますが、arctan(1/x)の式に直してみますと、
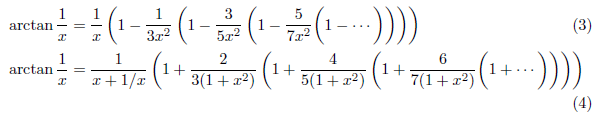
となり、結構似ていることが分かります。(式(3)は式(1)より、また式(4)は式(2)より得られます。)
式(3)の場合
このとき、Binary Splitting法の計算に必要なAi、Bi、Ciは、次のようになります。
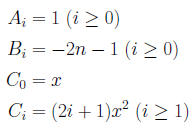
再帰版のプログラムでは、この定義でコーディングしますが、非再帰版のプログラムでは、まず![]() とし、ついでi=1...L-1まで
とし、ついでi=1...L-1まで
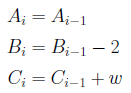
とし、最後に![]() とします。最初に非再帰版の十進BASICのプログラムを示します。足し合わせる項の数が、arctan(1/49)の項L(1)が2^7、arctan(1/57)の項L(2)が2^7、arctan(1/239)の項L(3)が2^7、arctan(1/110443)の項L(4)が2^6のとき、小数点以下438桁の精度があります。
とします。最初に非再帰版の十進BASICのプログラムを示します。足し合わせる項の数が、arctan(1/49)の項L(1)が2^7、arctan(1/57)の項L(2)が2^7、arctan(1/239)の項L(3)が2^7、arctan(1/110443)の項L(4)が2^6のとき、小数点以下438桁の精度があります。
PiTakano_MadhavaGregoryLeibniz.BAS
1: ! 高野の公式による円周率の計算 2: ! 非再帰版 Binary splitting 3: OPTION BASE 0 4: OPTION ARITHMETIC DECIMAL_HIGH 5: 6: ! atn(1/x) を計算する外部関数の宣言 7: DECLARE EXTERNAL FUNCTION atnR 8: 9: LET term = 4 10: DIM F(0 TO term-1) 11: DIM X(0 TO term-1) 12: DIM L(0 TO term-1) 13: ! 第1項 14: LET F(0) = 48 15: LET X(0) = 49 16: LET L(0) = 2^7 ! 足し合わせる項の数は2^nの形 17: ! 第2項 18: LET F(1) = 128 19: LET X(1) = 57 20: LET L(1) = 2^7 ! 足し合わせる項の数は2^nの形 21: ! 第3項 22: LET F(2) =-20 23: LET X(2) = 239 24: LET L(2) = 2^7 ! 足し合わせる項の数は2^nの形 25: ! 第4項 26: LET F(3) = 48 27: LET X(3) = 110443 28: LET L(3) = 2^6 ! 足し合わせる項の数は2^nの形 29: 30: LET pai = 0.0 31: FOR i = 0 TO term-1 32: LET pai = pai + F(i) * atnR(X(i), L(i)) 33: NEXT i 34: PRINT pai 35: !PRINT pai - PI 36: END 37: 38: ! atn(1/x)を計算する外部関数 39: EXTERNAL FUNCTION atnR(x, L) 40: OPTION ARITHMETIC DECIMAL_HIGH 41: DIM A(0 TO L-1) 42: DIM B(0 TO L-1) 43: DIM C(0 TO L-1) 44: 45: ! 配列 A(), B(), C() のセット 46: LET A(0) = 1 47: LET B(0) = -1 48: LET C(0) = x^2 49: LET w = 2 * C(0) 50: FOR i = 1 TO L-1 51: LET A(i) = A(i-1) 52: LET B(i) = B(i-1) - 2 53: LET C(i) = C(i-1) + w 54: NEXT i 55: LET C(0) = x ! C(0) = C(0) / x 56: 57: ! 繰り返し計算 58: LET n = L / 2 59: DO WHILE n >= 1 60: FOR i = 0 TO n-1 61: LET A(i) = A(2 * i) * C(2 * i + 1) + B(2 * i) * A(2 * i + 1) 62: LET B(i) = B(2 * i) * B(2 * i + 1) 63: LET C(i) = C(2 * i) * C(2 * i + 1) 64: NEXT i 65: LET n = n / 2 66: LOOP 67: LET atnR = A(0) / C(0) 68: END function
次に、再帰版の十進BASICのプログラムを示します。足し合わせる項の数が、arctan(1/49)の項L(1)が183、arctan(1/57)の項L(2)が179、arctan(1/239)の項L(3)が148、arctan(1/110443)の項L(4)が85のとき、小数点以下624桁の精度があります。
PiTakano_MadhavaGregoryLeibnizR.BAS
1: ! 高野の公式による円周率の計算 2: ! 再帰版 Binary splitting 3: OPTION ARITHMETIC decimal_high 4: DECLARE EXTERNAL SUB RecursiveAtnR 5: DIM XX(1 TO 3) 6: LET A = 1 7: LET B = 2 8: LET C = 3 9: LET XX(A) = 0 10: LET XX(B) = 0 11: LET XX(C) = 0 12: 13: DIM f(1 TO 4) 14: DIM x(1 TO 4) 15: DIM L(1 TO 4) 16: ! 第1項 17: LET f(1) = 48 18: LET x(1) = 49 19: LET L(1) = 183 ! 足し合わせる項の数は2^nの形でなくてもよい 20: ! 第2項 21: LET f(2) = 128 22: LET x(2) = 57 23: LET L(2) = 179 ! 足し合わせる項の数は2^nの形でなくてもよい 24: ! 第3項 25: LET f(3) = -20 26: LET x(3) = 239 27: LET L(3) = 148 ! 足し合わせる項の数は2^nの形でなくてもよい 28: ! 第4項 29: LET f(4) = 48 30: LET x(4) = 110443 31: LET L(4) = 85 ! 足し合わせる項の数は2^nの形でなくてもよい 32: 33: LET pai = 0 34: FOR i = 1 TO 4 35: CALL RecursiveAtnR(0, L(i), XX, x(i)) 36: LET pai = pai + f(i) * XX(A) / XX(C) 37: NEXT i 38: PRINT pai 39: !PRINT pai - PI 40: 41: END 42: 43: EXTERNAL SUB RecursiveAtnR(n0, n1, Q(), x) 44: OPTION ARITHMETIC decimal_high 45: DIM left(1 TO 3) 46: DIM right(1 TO 3) 47: 48: LET A = 1 49: LET B = 2 50: LET C = 3 51: 52: LET left(A) = 0 53: LET left(B) = 0 54: LET left(C) = 0 55: LET right(A) = 0 56: LET right(B) = 0 57: LET right(C) = 0 58: 59: IF n1 - n0 = 1 THEN 60: LET Q(A) = 1 61: LET Q(B) = -2 * n0 - 1 62: LET Q(C) = (2 * n0 + 1) * x * x 63: IF n0 = 0 THEN 64: LET Q(C) = x 65: END IF 66: EXIT SUB 67: END IF 68: 69: LET mid = INT((n0 + n1) / 2) 70: 71: CALL RecursiveAtnR(n0, mid, left, x) 72: CALL RecursiveAtnR(mid, n1, right, x) 73: 74: LET Q(A) = left(A) * right(C) + left(B) * right(A) 75: LET Q(B) = left(B) * right(B) 76: LET Q(C) = left(C) * right(C) 77: 78: END SUB
式(4)の場合
このとき、Binary Splitting法の計算に必要なAi、Bi、Ciは、次のようになります。
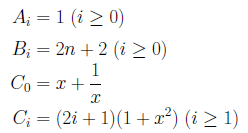
再帰版のプログラムでは、この定義でコーディングしますが、非再帰版のプログラムでは、まず![]() とし、ついでi=1...L-1まで
とし、ついでi=1...L-1まで
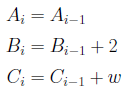
とし、最後に![]() とします。最初に非再帰版の十進BASICのプログラムを示します。足し合わせる項の数arctan(1/49)の項L(1)が2^7、arctan(1/57)の項L(2)が2^7、arctan(1/239)の項L(3)が2^7、arctan(1/110443)の項L(4)が2^6のとき、小数点以下436桁の精度があります。
とします。最初に非再帰版の十進BASICのプログラムを示します。足し合わせる項の数arctan(1/49)の項L(1)が2^7、arctan(1/57)の項L(2)が2^7、arctan(1/239)の項L(3)が2^7、arctan(1/110443)の項L(4)が2^6のとき、小数点以下436桁の精度があります。
PiTakano_Euler.BAS
1: ! 高野の公式による円周率の計算 2: ! 非再帰版 Binary splitting 3: OPTION BASE 0 4: OPTION ARITHMETIC DECIMAL_HIGH 5: 6: ! atn(1/x) を計算する外部関数の宣言 7: DECLARE EXTERNAL FUNCTION atnR 8: 9: LET term = 4 10: DIM F(0 TO term-1) 11: DIM X(0 TO term-1) 12: DIM L(0 TO term-1) 13: ! 第1項 14: LET F(0) = 48 15: LET X(0) = 49 16: LET L(0) = 2^7 ! 足し合わせる項の数は2^nの形 17: ! 第2項 18: LET F(1) = 128 19: LET X(1) = 57 20: LET L(1) = 2^7 ! 足し合わせる項の数は2^nの形 21: ! 第3項 22: LET F(2) =-20 23: LET X(2) = 239 24: LET L(2) = 2^7 ! 足し合わせる項の数は2^nの形 25: ! 第4項 26: LET F(3) = 48 27: LET X(3) = 110443 28: LET L(3) = 2^6 ! 足し合わせる項の数は2^nの形 29: 30: LET pai = 0.0 31: FOR i = 0 TO term-1 32: LET pai = pai + F(i) * atnR(X(i), L(i)) 33: NEXT i 34: PRINT pai 35: !PRINT pai - PI 36: END 37: 38: ! atn(1/x)を計算する外部関数 39: EXTERNAL FUNCTION atnR(x, L) 40: OPTION ARITHMETIC DECIMAL_HIGH 41: DIM A(0 TO L-1) 42: DIM B(0 TO L-1) 43: DIM C(0 TO L-1) 44: 45: ! 配列 A(), B(), C() のセット 46: LET A(0) = 1 47: LET B(0) = 2 48: LET C(0) = 1 + x^2 49: LET w = 2 * C(0) 50: FOR i = 1 TO L-1 51: LET A(i) = A(i-1) 52: LET B(i) = B(i-1) + 2 53: LET C(i) = C(i-1) + w 54: NEXT i 55: LET C(0) = C(0) / x 56: 57: ! 繰り返し計算 58: LET n = L / 2 59: DO WHILE n >= 1 60: FOR i = 0 TO n-1 61: LET A(i) = A(2 * i) * C(2 * i + 1) + B(2 * i) * A(2 * i + 1) 62: LET B(i) = B(2 * i) * B(2 * i + 1) 63: LET C(i) = C(2 * i) * C(2 * i + 1) 64: NEXT i 65: LET n = n / 2 66: LOOP 67: LET atnR = A(0) / C(0) 68: END function
次に、再帰版の十進BASICのプログラムを示します。足し合わせる項の数が、arctan(1/49)の項L(1)が183、arctan(1/57)の項L(2)が179、arctan(1/239)の項L(3)が148、arctan(1/110443)の項L(4)が85のとき、小数点以下622桁の精度があります。
PiTakano_EulerR.BAS
1: ! 高野の公式による円周率の計算 2: ! 再帰版 Binary splitting 3: OPTION ARITHMETIC decimal_high 4: DECLARE EXTERNAL SUB RecursiveAtnR 5: DIM XX(1 TO 3) 6: LET A = 1 7: LET B = 2 8: LET C = 3 9: LET XX(A) = 0 10: LET XX(B) = 0 11: LET XX(C) = 0 12: 13: DIM f(1 TO 4) 14: DIM x(1 TO 4) 15: DIM L(1 TO 4) 16: ! 第1項 17: LET f(1) = 48 18: LET x(1) = 49 19: LET L(1) = 183 ! 足し合わせる項の数は2^nの形でなくてもよい 20: ! 第2項 21: LET f(2) = 128 22: LET x(2) = 57 23: LET L(2) = 179 ! 足し合わせる項の数は2^nの形でなくてもよい 24: ! 第3項 25: LET f(3) = -20 26: LET x(3) = 239 27: LET L(3) = 148 ! 足し合わせる項の数は2^nの形でなくてもよい 28: ! 第4項 29: LET f(4) = 48 30: LET x(4) = 110443 31: LET L(4) = 85 ! 足し合わせる項の数は2^nの形でなくてもよい 32: 33: LET pai = 0 34: FOR i = 1 TO 4 35: CALL RecursiveAtnR(0, L(i), XX, x(i)) 36: LET pai = pai + f(i) * XX(A) / XX(C) 37: NEXT i 38: PRINT pai 39: !PRINT pai - PI 40: 41: END 42: 43: EXTERNAL SUB RecursiveAtnR(n0, n1, Q(), x) 44: OPTION ARITHMETIC decimal_high 45: DIM left(1 TO 3) 46: DIM right(1 TO 3) 47: 48: LET A = 1 49: LET B = 2 50: LET C = 3 51: 52: LET left(A) = 0 53: LET left(B) = 0 54: LET left(C) = 0 55: LET right(A) = 0 56: LET right(B) = 0 57: LET right(C) = 0 58: 59: IF n1 - n0 = 1 THEN 60: LET Q(A) = 1 61: LET Q(B) = 2 * n0 + 2 62: LET Q(C) = (2 * n0 + 1) * (1 + x * x) 63: IF n0 = 0 THEN 64: LET Q(C) = x + 1 / x 65: END IF 66: EXIT SUB 67: END IF 68: 69: LET mid = INT((n0 + n1) / 2) 70: 71: CALL RecursiveAtnR(n0, mid, left, x) 72: CALL RecursiveAtnR(mid, n1, right, x) 73: 74: LET Q(A) = left(A) * right(C) + left(B) * right(A) 75: LET Q(B) = left(B) * right(B) 76: LET Q(C) = left(C) * right(C) 77: 78: END SUB