はじめに
Ｇａｍｍａ関数とは、次の式で表される特殊関数です。
よく知られているように、ガンマ関数は階乗の拡張になっており、次の関係式が成り立ち
ます。
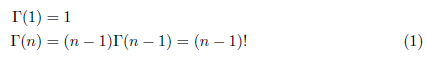
また、次に示すベータ関数B は、ガンマ関数を用いて、次のように表されます。
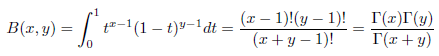
x = y = 1/2 のとき
x = y = 1/2 のとき、次のようになります。
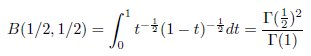
ここで、
とおくと、
となるので、
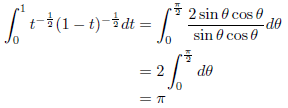
となります。従って、
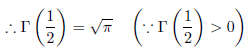
であることが分かります。さらに、
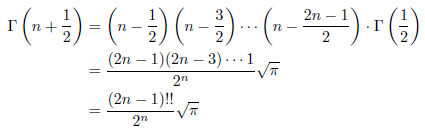
となることも分かります。
この結果と式(1) を用いると、次の結果が導かれます。n ≥ 1 のとき、
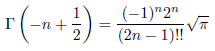
となります。
ここで、次の式を定義します。n > 0 のとき、
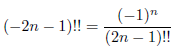
とします。例えば、
です。このように定義すると、全ての n で、
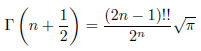
が成立します。いくつか例示しますと、
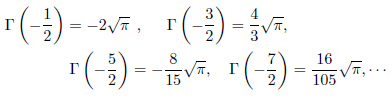
となります。
x = (q + 1)/p, y = 1/2 のとき
このとき、
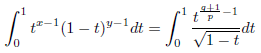
となります。ここで
と置換すると、
となるため、
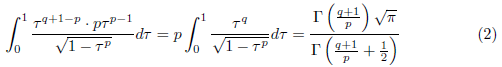
となります。
無限級数展開その1
式(2)より、
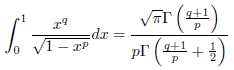
となりますが、一方、
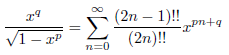
となります。したがって、
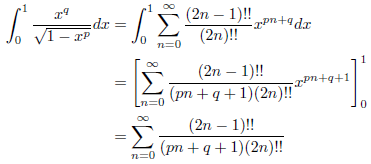
が成り立ちます。
特にp = 4, q = 4k + 1 のとき、
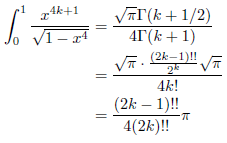
となります。一方、
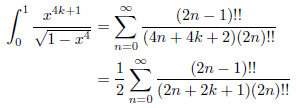
です。従って、
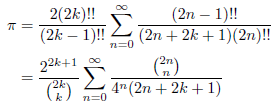
となります。例えばk = 0, 1, 2 のとき、
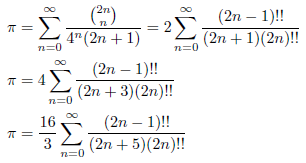
が成立します。
これらの無限級数展開は、直接ベータ関数を無限級数展開しても得られます。
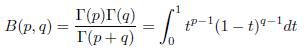
において、(1 - t)q - 1 を無限級数展開すると、
となるので、
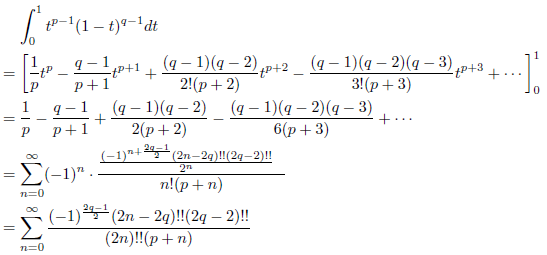
となります。
p = q = 1/2 のとき、無限級数展開は次のようになります。
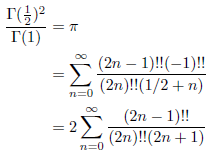
p = 3/2, q = 1/2 のとき、無限級数展開は次のようになります。
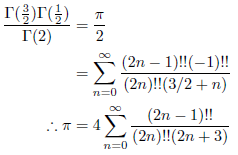
p = 5/2, q = 1/2 のとき、無限級数展開は次のようになります。
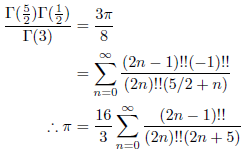
これらの式は、先に挙げた無限級数展開に他なりません。
次に、十進BASIC のプログラムを示します。収束が大変遅いことが確認できます。
Gamma1.BAS
1: OPTION ARITHMETIC DECIMAL 2: ! n=0 3: LET DblFact = 1 4: LET n = 0 5: LET s1 = 2 * DblFact / (2 * n + 1) 6: LET s2 = 4 * DblFact / (2 * n + 3) 7: LET s3 = 16 / 3 * DblFact / (2 * n + 5) 8: PRINT " n k = 0 k = 1 k = 2" 9: PRINT USING "####### #.##### #.##### #.#####":n, s1, s2, s3 10: 11: FOR n = 1 TO 1000000 12: LET DblFact = DblFact * (2 * n - 1) / 2 / n 13: LET s1 = s1 + 2 * DblFact / (2 * n + 1) 14: LET s2 = s2 + 4 * DblFact / (2 * n + 3) 15: LET s3 = s3 + 16 / 3 * DblFact / (2 * n + 5) 16: IF MOD(n, 100000) = 0 THEN 17: PRINT USING "####### #.##### #.##### #.#####":n, s1, s2, s3 18: END IF 19: NEXT n 20: END
無限級数展開その2
この節では、オイラーの関数等式
をもとに無限級数展開を求めます。0 < x < 1 で、次の式が成り立ちます。
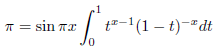
ここで、
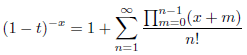
を利用して無限級数展開しますと、
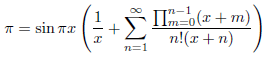
が得られます。
たとえばx = 1/6 のとき、
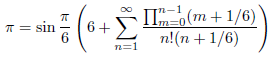
となります。従って、
より、
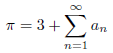
が得られます。
次に、十進BASIC のプログラムを示します。こちらのプログラムも、収束が遅いことが分かります。
Gamma2.BAS
1: OPTION ARITHMETIC DECIMAL 2: ! 初期設定 3: LET a = 1 / 14 4: LET s = 3 + a 5: PRINT USING "#### #.############":1,s 6: 7: ! 繰り返し 8: FOR n = 2 TO 4000 9: LET a = (6 * n - 5)^2 / 6 / n / (6 * n + 1) * a 10: LET s = s + a 11: PRINT USING "#### #.############":n,s 12: next n 13: END