こつこつアルゴリズム(Spigot Algorithm)

概要

円周率の値を計算するためには、多倍長計算をしなければならないと思われていました。ところが、こつこつアルゴリズムを用いると、特別に多倍長計算をしなくてもよいことが示されました。

最初に、こつこつアルゴリズムの概要について示します。このアルゴリズムでは、次の級数を基にして計算します。

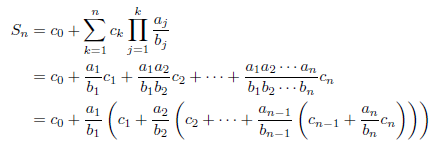
ここで、divを整数商、modを剰余としますと、(例えば、となります)

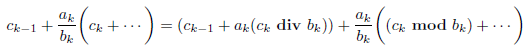
が成り立ちます。こつこつアルゴリズムでこの関係をどう用いるか、最初にネイピア数を例に、示すことにします。まず、小数点以下1桁目の1を抽出します。式中の青色の部分にご注目ください。

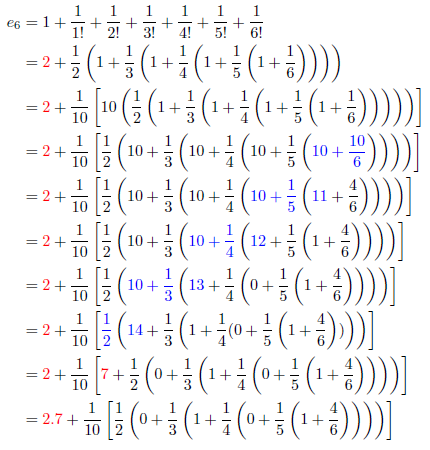
これで、7が抽出できました。引き続き、小数点以下2桁目の1を抽出してみます。

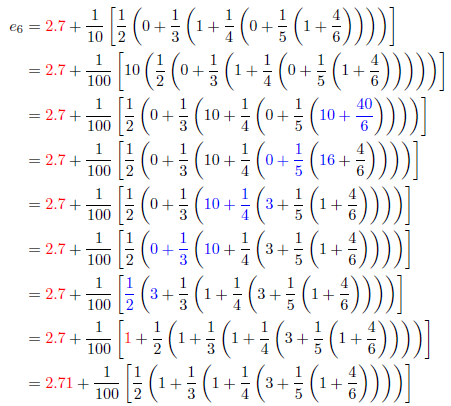
この手続きを繰り返すことにより、多倍長計算をせずに小数点以下の数を求めることができるわけです。実際には、繰り上がりの処理等をしなければなりませんが、本質はここで述べた計算にあります。

もちろん、円周率についてもこの計算法を適用できます。ここでは、Gosper による次の級数を取り上げて見ます。

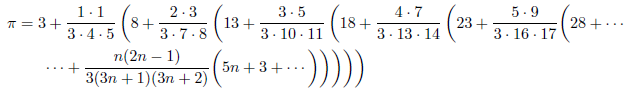
この無限級数の部分和

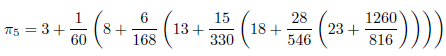
を考えます。先ほどと同様に計算してみましょう。

小数点以下2桁を抽出できました。

ここで、お気づきの方もいらっしゃるかもしれませんが、抽出は1 桁ずつ行う必要はありません。次に3 桁ずつ抽出してみます。

小数点以下6桁を抽出することができました。

アルゴリズムその1

次に示すC言語のプログラムは、短いにも拘らず15000桁の円周率を求めることができます。

long a[52514],b,c=52514,d,e,f=1e4,g,h;
main(){for(;b=c-=14;h=printf("%04d",e+d/f))
for(e=d%=f;g=--b*2;d/=g)
d=d*b+f*(h?a[b]:f/5),a[b]=d%--g;}

十進BASICでも、こつこつアルゴリズムのプログラムを書くことができます。十進1000桁モードにする必要はありません。入力桁数によっては、計算に長時間かかりますのでご注意ください。

PiSpigot.BAS

   1: !こつこつアルゴリズムを用いて、円周率を求める。
   2: OPTION BASE 0
   3: 
   4: INPUT PROMPT "計算したい桁数 ":n
   5: PRINT "円周率を";n - MOD(n, 4);"桁求める。"
   6: LET L = (INT(n / 4) + 1) * 14
   7: DIM a(L)
   8: LET c = L
   9: LET d = 0
  10: LET e = 0
  11: LET f = 10000
  12: 
  13: ! first loop
  14: LET c = c - 14
  15: LET b = c
  16: LET b = b - 1
  17: DO WHILE b > 0                           !inner loop: radix conv
  18:    LET d = d * b                         !acc *= nom. prev base
  19:    LET d = d + 2000 * f                  !first outer loop
  20:    LET g = b + b - 1                     !denom. prev base
  21:    LET a(b) = MOD(d, g)
  22:    LET d = INT(d / g)                    !save carry
  23:    LET b = b - 1
  24: LOOP
  25: PRINT USING "#.###":INT(e + d / f)/1000; !print prev 4 digits
  26: LET e = MOD(d, f)                        !save current 4 digits
  27: LET d = e                                !assure a small enough d
  28: LET c = c - 14
  29: LET b = c
  30: 
  31: ! second to last loop
  32: DO WHILE b > 0                           !outer loop: 4 digits/loop
  33:    LET b = b - 1
  34:    DO WHILE b > 0                        !inner loop: radix conv.
  35:       LET d = d * b                      !acc *= nom. prev base
  36:       LET d = d + a(b) * f               !non-first outer loop
  37:       LET g = b + b - 1                  !denom. prev base
  38:       LET a(b) = MOD(d, g)
  39:       LET d = INT(d / g)                 !save carry
  40:       LET b = b - 1
  41:    LOOP
  42:    PRINT USING "%%%%":INT(e + d / f);    !print prev 4 digits
  43:    LET e = MOD(d, f)                     !save current 4 digits
  44:    LET d = e                             !assure a small enough d
  45:    LET c = c - 14
  46:    LET b = c
  47: LOOP
  48: 
  49: END

アルゴリズムその2

また、最近J.Gibbonsにより、新しいこつこつアルゴリズムのプログラムが示されました。Haskellというプログラミング言語でコーディングされていました。

piG3 = g(1,180,60,2) where
  g(q,r,t,i) =
    let (u,y)=(3*(3*i+1)*(3*i+2),div(q*(27*i-12)+5*r)(5*t))
    in y : g(10*q*i*(2*i-1),10*u*(q*(5*i-2)+r-y*t),t*u,i+1)
main = print piG3

このプログラムでは、パソコンが止まるまで無限に動き続けます。1000桁のみ計算させたい場合は、最終行を

main = print $ take 1000 piG3

PiSpigotGibbons.BAS

   1: !こつこつアルゴリズム(Gibbons)を用いて、円周率を求める。
   2: 
   3: INPUT PROMPT "計算したい桁数 ":n
   4: PRINT "円周率を";n;"桁求める。"
   5: 
   6: LET q1 = 1
   7: LET r1 = 180
   8: LET t1 = 60
   9: LET i1 = 2
  10: LET u1 = 3 * (3 * i1 + 1) * (3 * i1 + 2)
  11: LET y1 = INT((q1 * (27 * i1 - 12) + 5 * r1) / 5 / t1)
  12: PRINT USING "#.":y1;
  13: 
  14: FOR i = 1 TO n
  15:    LET q2 = 10 * q1 * i1 * (2 * i1 - 1)
  16:    LET r2 = 10 * u1 * (q1 * (5 * i1 - 2) + r1 - y1 * t1)
  17:    LET t2 = t1 * u1
  18:    LET i2 = i1 + 1
  19:    LET u2 = 3 * (3 * i2 + 1) * (3 * i2 + 2)
  20:    LET y2 = INT((q2 * (27 * i2 - 12) + 5 * r2) / 5 / t2)
  21:    PRINT USING "#":y2;
  22:    LET q1 = q2
  23:    LET r1 = r2
  24:    LET t1 = t2
  25:    LET i1 = i2
  26:    LET u1 = u2
  27:    LET y1 = y2
  28: NEXT i
  29: 
  30: END

そこで、Haskell処理系のひとつであるGHCで実行ファイルを作成してみました。コマンドプロンプトからpiG3.exeを実行してみてください。マシンが停止するまで無限に計算しますので、適当なところでCtrl+Cキーにて実行を止めてください。

ダウンロードはこちらから ==>