反復法
反復法は、固定点![]() の解xを求める方法であり、古典的な非線形方程式の解法として知られています。反復の式は、
の解xを求める方法であり、古典的な非線形方程式の解法として知られています。反復の式は、
![]()
であり、この式が収束する条件は![]() です。
です。
Steffensenの方法
一方、Steffensenの方法は、同じく![]() の解xを求める方法ですが、収束を速めるためにAitkenのΔ2法をもとに導かれました。漸化式は、
の解xを求める方法ですが、収束を速めるためにAitkenのΔ2法をもとに導かれました。漸化式は、
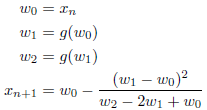
となり、xnは、2次収束することが知られています。特に![]() としたとき、
としたとき、
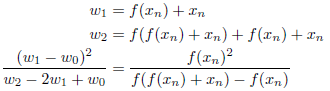
となりますので、結局
![]()
と表されます。この式は、
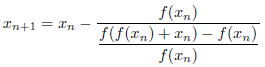
と変形できることから、Steffensen法は、Newton法の![]() を
を
![]()
で近似した方法であると考えられます。次に、平方根を求めるための漸化式を導きます。
最初の例
特に、![]() のとき、
のとき、
![]()
なので、
![]()
であり、a=2の場合、
![]()
となります。
別のg(x)の例
一方、![]() より、
より、
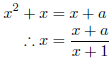
となるので、![]() とおくと、
とおくと、![]() であり、
であり、
![]()
となります。したがって、この場合の漸化式は、
![]()
となります。古典的な反復法とSteffensen法の違いを体感していただくために、十進BASICのプログラムを作成してみました。次に示します。
C:\BASICprograms\sqrt\Steffensen1.BAS
1: ! 単純な反復法とSteffensen法を比較する。 2: OPTION ARITHMETIC DECIMAL 3: 4: INPUT PROMPT "平方根を計算したい数 a = ":a 5: 6: ! 初期値 (x : 通常の反復法、y : Steffensenの方法) 7: LET x = 1 8: LET y = 1 9: 10: PRINT " i 通常の反復法 Steffensenの方法" 11: PRINT USING "### ##.############ ##.############":i,x,y 12: 13: ! iをカウンタとする 14: LET i = 0 15: DO 16: LET x = (x + a) / (x + 1) 17: LET y = y - (y^2 - a) * (2 * y + a + 1) / 2 / (y + a) / (y + 1) 18: LET i = i + 1 19: PRINT USING "### ##.############ ##.############":i,x,y 20: LOOP WHILE ABS(x - y) > 0.000000000001 21: 22: END
別のg(x)の例
一方、![]() より、
より、
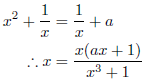
となるので、![]() とおくと、
とおくと、![]() であり、
であり、
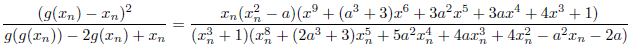
となります。したがって、この場合の漸化式は、
![]()
となります。
別のg(x)の例
一方、![]() より、
より、
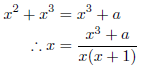
となるので、![]() とおくと、この場合の漸化式は、
とおくと、この場合の漸化式は、
![]()
となります。