高次の方法1

方法その1

収束の次数が2以上の方法を導きます[21]。はじめに、次のマクローリン展開を考えます。

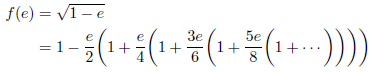
この式を途中で打ち切って、漸化式を求めます。のとき、

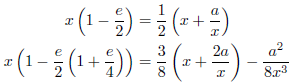
などとなります。上の式からはNewton法の漸化式が、下の式からはChebyshev法の漸化式が得られる。さらに高次の式も同様に、

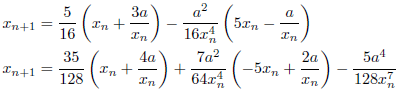
と求めることができます。十進BASICのプログラムを次に示します。

HigherOrder1.BAS

   1: !
   2: ! 平方根を収束計算により求める。
   3: !
   4: ! 入力
   5: !  a : 平方根を求めたい数
   6: !  m : 収束の次数(m = 2, 3, 4, 5, 6)
   7: !      m=2:Newton, m=3:Chebyshev
   8: !  x0: 初期値
   9: !
  10: OPTION ARITHMETIC DECIMAL_HIGH
  11: DECLARE EXTERNAL FUNCTION iter
  12: 
  13: INPUT PROMPT " 平方根を求めたい数 a = " : a
  14: INPUT PROMPT " 収束の次数 m(2,3,4,5,6)= " : m
  15: LET m = INT(m)
  16: IF m < 2 THEN LET m = 2
  17: IF m > 6 THEN LET m = 6
  18: INPUT PROMPT " 初期値 x0 = " : x0
  19: 
  20: LET i = 0
  21: PRINT i, x0
  22: DO
  23:    LET x = x0
  24:    LET x0 = iter(a, x0, m)
  25:    LET i = i + 1
  26:    PRINT i, x0
  27: LOOP WHILE ABS(x - x0) > 1e-1000
  28: END
  29: 
  30: EXTERNAL FUNCTION iter(a, x, m)
  31: OPTION ARITHMETIC DECIMAL_HIGH
  32: SELECT CASE m
  33: CASE 2
  34:    LET iter = (x + a / x) / 2
  35: CASE 3
  36:    LET iter = 3 / 8 * (x + 2 * a / x) - a^2 / 8 / x^3
  37: CASE 4
  38:    LET iter = 5 / 16 * (x + 3 * a / x) - a^2 / 16 / x^4 * (5 * x - a / x)
  39: CASE 5
  40:    LET iter = 35 / 128 * (x + 4 * a / x) - 7 * a^2 / 64 / x^4 * (5 * x - 2 * a / x)
         - 5 * a^4 / 128 / x^7
  41: CASE 6
  42:    LET iter = 63 / 256 * (x + 5 * a / x) - 21 * a^2 / 128 / x^4 * (5 * x - 3 * a / x)
         - a^4 / 256 / x^8 *(45 * x - 7 * a / x)
  43: END SELECT
  44: END FUNCTION

方法その2

今度は、のマクローリン展開を考えます。記号

を用いて、

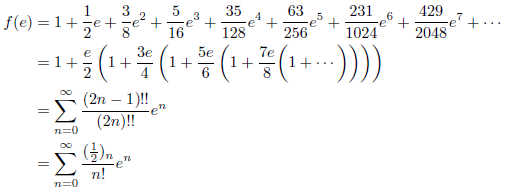
と表せます。aの平方根を求めるためには、まずを求め、ついでにaをかければよい。そこでとして、次の漸化式

によりを求めます。

2次収束の場合

このとき、漸化式は次のようになります。

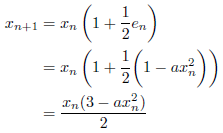
したがって、となります。

4次収束の場合

このとき、漸化式は次のようになります。

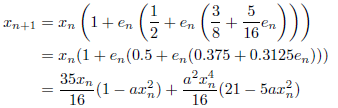
したがって、となります。

8次収束の場合

このとき、漸化式は次のようになります。

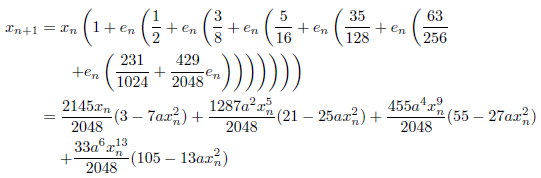
したがって、となります。十進BASICのプログラムを次に示します。

HigherOrder2.BAS

   1: !
   2: ! 平方根を収束計算により求める。
   3: !
   4: ! 入力
   5: !  a : 平方根を求めたい数
   6: !  m : 収束の次数(m = 2, 3, 4, 5, 6)
   7: !
   8: !  x0: 初期値
   9: !
  10: OPTION ARITHMETIC DECIMAL_HIGH
  11: DECLARE EXTERNAL FUNCTION iter
  12: 
  13: INPUT PROMPT " 平方根を求めたい数 a = " : a
  14: INPUT PROMPT " 収束の次数 m(2,3,4,5,6)= " : m
  15: LET m = INT(m)
  16: IF m < 2 THEN LET m = 2
  17: IF m > 6 THEN LET m = 6
  18: INPUT PROMPT " 初期値 x0 = " : x0
  19: 
  20: LET i = 0
  21: PRINT i, x0
  22: DO
  23:    LET x = x0
  24:    LET x0 = iter(a, x0, m)
  25:    LET i = i + 1
  26:    PRINT i, a * x0
  27: LOOP WHILE ABS(x - x0) > 1e-1000
  28: END
  29: 
  30: EXTERNAL FUNCTION iter(a, x, m)
  31: OPTION ARITHMETIC DECIMAL_HIGH
  32: SELECT CASE m
  33: CASE 2
  34:    LET iter = x * (3 - a * x^2) / 2
  35: CASE 3
  36:    LET iter = 5 * x * (3 - 2 * a * x^2) / 8 + 3 * a^2 * x^5 / 8
  37: CASE 4
  38:    LET iter = 35 * x * (1 - a * x^2) / 16 + a^2 * x^5 * (21 - 5 * a * x^2) / 16
  39: CASE 5
  40:    LET iter = 105 * x * (3 - 4 * a * x^2) / 128
         + 9 * a^2 * x^5 * (21 - 10 * a * x^2) / 64 + 35 * a^4 * x^9 / 128
  41: CASE 6
  42:    LET iter = 231 * x * (3 - 5 * a * x^2) / 256
          + 99 * a^2 * x^5 * (7 - 5 * a * x^2) / 128 
          + 7 * a^4 * x^9 * (55 - 9 * a * x^2) / 256
  43: END SELECT
  44: END FUNCTION