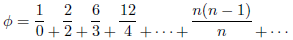平方根の場合
これまでの連分数と漸化式の議論で、
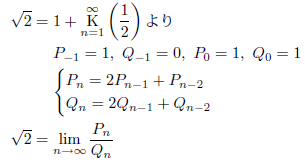
ならびに
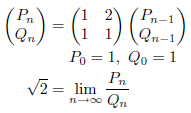
と表されることが分かりました。ここでは、参考文献[5,p291]に従って、連分数![]() に対する
に対する
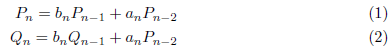
と漸化式
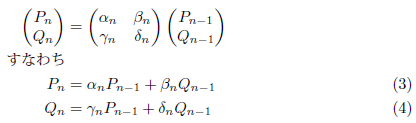
の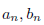 と
と![]() との間に、どのような関係があるか考察します。また、
との間に、どのような関係があるか考察します。また、![]() を
を![]() を用いて表してみます。まず(3),(4)より、
を用いて表してみます。まず(3),(4)より、
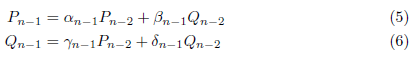
が成り立ちます。(5)より、![]() のとき、
のとき、
![]()
となります。(6)に代入すると、
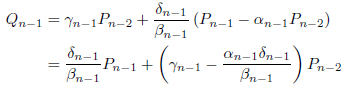
となります。(3)に代入すると、
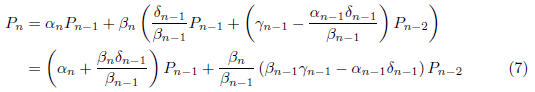
が得られます。一方(6)より、![]() のとき、
のとき、
![]()
となります。(5)に代入して、
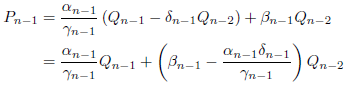
となります。(4)に代入して、
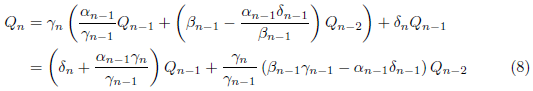
が得られます。(1)(2)(7)(8)より、![]() において、
において、
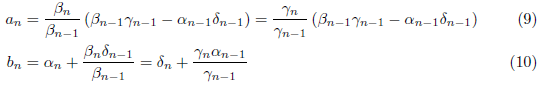
が成り立ちます。ここで(9)より、![]() となります。よって、
となります。よって、
![]()
となります。したがって![]() とおくと、
とおくと、![]() となります。一方(10)より、
となります。一方(10)より、
![]()
となり、
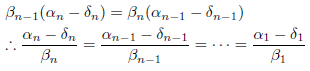
となります。したがって、![]() とおくと、
とおくと、![]() となります。すなわち
となります。すなわち
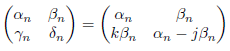
となります。まとめますと、![]() で
で
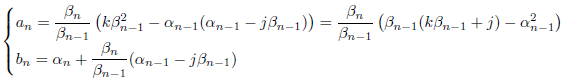
が得られます。一方、![]() なので、
なので、
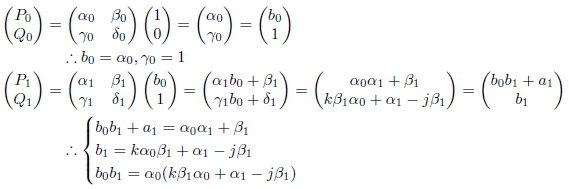
となります。したがって、
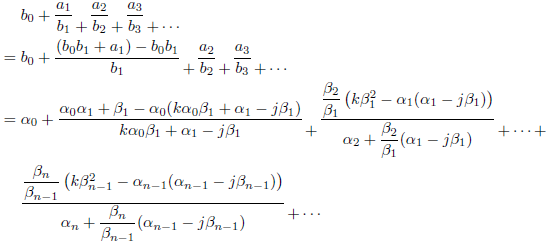
となります。次にいくつかの例を示します。
j=0, k=1/2の場合
このとき、2γn=βn,δn=αnとなります。行列Aを、
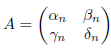 としますと、
としますと、![]() の連分数展開が得られます。いくつかの例を示します。
の連分数展開が得られます。いくつかの例を示します。
例1
![]() のとき
のとき![]() であり、連分数は次のようになります。
であり、連分数は次のようになります。
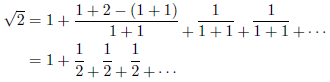
例2
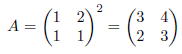 のとき
のとき![]() であり、連分数は次のようになります。
であり、連分数は次のようになります。
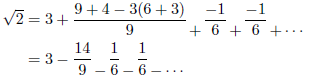
例3
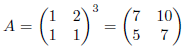 のとき
のとき![]() であり、連分数は次のようになります。
であり、連分数は次のようになります。
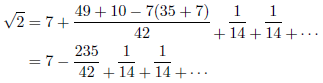
例4
![]() のとき
のとき![]() であり、連分数は次のようになります。
であり、連分数は次のようになります。
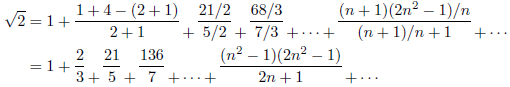
例5
![]() のとき
のとき![]() であり、連分数は次のようになります。
であり、連分数は次のようになります。
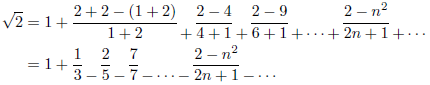
例6
![]() のとき
のとき![]() であり、連分数は次のようになります。
であり、連分数は次のようになります。
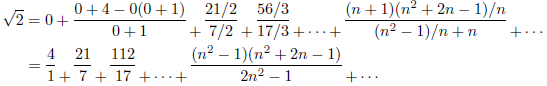
j=k=1の場合
つぎに、j=k=1の場合を考えます。このとき、次の行列Aが得られます。
![]()
一方、黄金比の値を![]() としますと、この行列Aにより決まるPn、Qnを用いて、
としますと、この行列Aにより決まるPn、Qnを用いて、![]() となります。
となります。
今、Fibonacci数列を、![]() としますと、
としますと、
![]()
となることが確認できます。ここで、行列![]() は、先のAの条件(j = k = 1)を満たすため、黄金比を表す連分数を求めることができます。次にいくつかの例を挙げてみます。
は、先のAの条件(j = k = 1)を満たすため、黄金比を表す連分数を求めることができます。次にいくつかの例を挙げてみます。
例1
![]() のとき、連分数は次のようになります。
のとき、連分数は次のようになります。
![]()
例2
![]() のとき、連分数は次のようになります。
のとき、連分数は次のようになります。
![]()
例3
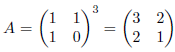 のとき、連分数は次のようになります。
のとき、連分数は次のようになります。
![]()
例4
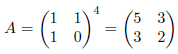 のとき、連分数は次のようになります。
のとき、連分数は次のようになります。
![]()
例5
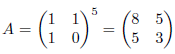 のとき、連分数は次のようになります。
のとき、連分数は次のようになります。
![]()
例6
![]() のとき、連分数は次のようになります。
のとき、連分数は次のようになります。
![]()
例7
![]() のとき、
のとき、![]() であり、連分数は次のようになります。
であり、連分数は次のようになります。
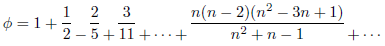
例8
![]() のとき、
のとき、![]() であり、連分数は次のようになります。
であり、連分数は次のようになります。
![]()
例9
![]() のとき、
のとき、![]() であり、連分数は次のようになります。
であり、連分数は次のようになります。
![]()
例10
![]() のとき、
のとき、![]() であり、連分数は次のようになります。
であり、連分数は次のようになります。