はじめに
このページでは、別の高次収束する方法を示します。得られる漸化式はどの方法でも同じです。
Gerlachの方法
参考文献[11]に記載の方法です。
の解を求めるとき、まず2次収束するNewton法から出発します。Newton法の繰り返しは、次のようになります。
ここで
を次の手順により生成します。
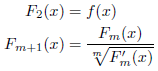
すると、
はm次収束すると記載されています。
m=2のとき
Newton法に等しくなります。
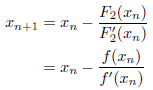
特に
のとき、上の式に代入して整理すると、
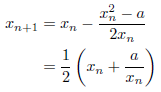
となります。
m=3のとき
Halley法に等しくなります。
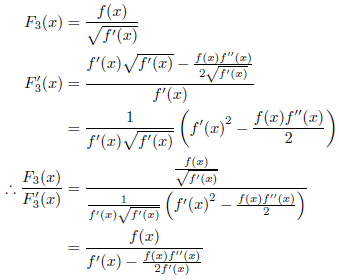
が成り立ちますので、次式が得られます。
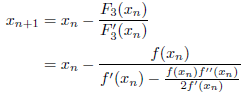
特にのとき、上の式に代入して整理すると、
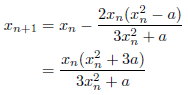
となります。
m=4のとき
次のようになります。
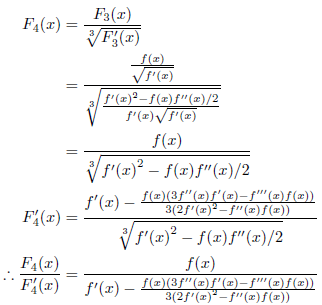
が成り立ちますので、次式が得られます。
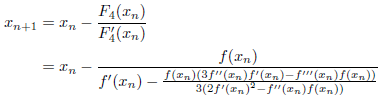
特にのとき、上の式に代入して整理すると、
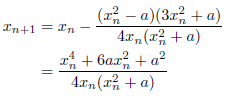
となります。
Ford, Pennlineの方法
前項のGerlachの方法では、
を求めるのがやや煩雑でした。参考文献[12]には、前項と等価な漸化式が、次の手順でより簡単に求められると記載されています。すなわち、
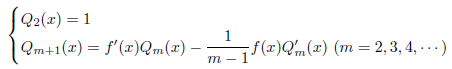
とすると、
はm次収束します。証明は、
を、次のように構成します。
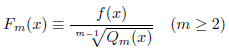
次に、を微分します。
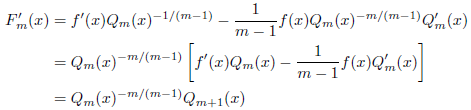
よって、次の量は
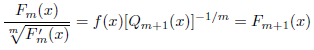
となるのでGerlachの条件を満たし、
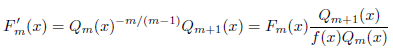
となるので、式(1)が成立し、m次収束します。
次に、の場合の
を求めます。
であることに注意しますと、
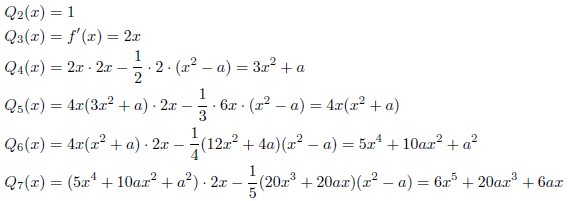
となります。次に、いくつかの式を導きます。
m=2のとき
Newton法に等しくなります。
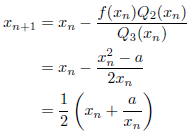
m=3のとき
Halley法と等価になります。
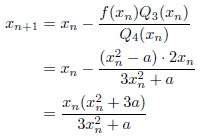
m=4のとき
次のようになります。
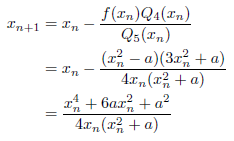
m=5のとき
次のようになります。
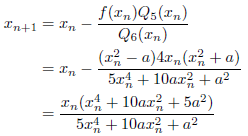
m=6のとき
次のようになります。
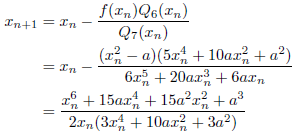
Kalantariの方法
参考文献[13]に記載の方法です。前項と等価な漸化式が得られます。次式がm次収束します。
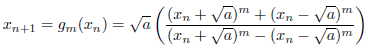
いくつかの場合について、例示します。
m=2のとき(2次収束)
Newton法と等価になります。
m=3のとき(3次収束)
Halley法と等価になります。
m=4のとき(4次収束)
次のようになります。
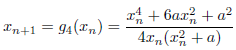
m=5のとき(5次収束)
次のようになります。
m=6のとき(6次収束)
次のようになります。
Dahlquist, Björkの方法
参考文献[7,p650]に記載の方法です。kを正の奇数として、aの平方根を求めるための漸化式は、次のようになります。
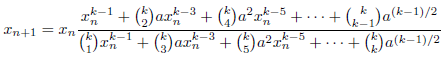
k=3のとき(3次収束)
Halley法と等価になります。
k=5のとき(5次収束)
次のようになります。
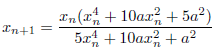
k=7のとき(7次収束)
次のようになります。
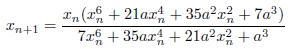
連分数に基づく方法
平方根の連分数展開をもとに漸化式を求めてみます。ここで取り上げる連分数展開は、
です。この展開式より、形式的に
とし、途中で打ち切ります。次に例を示します。
m=2のとき(2次収束)
Newton法と等価になります。
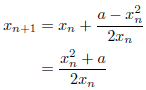
m=3のとき(3次収束)
Halley法と等価になります。
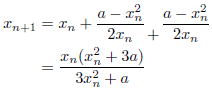
m=4のとき(4次収束)
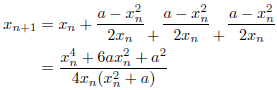
m=5のとき(5次収束)
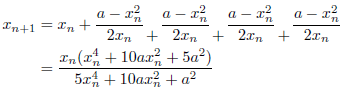
m=6のとき(6次収束)
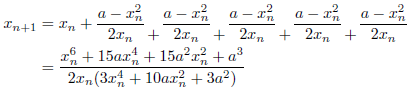
その他の方法
次の方法によっても、同じ漸化式が得られます。まず、
として、
によってgm(x)を定めると、
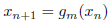
がm次収束することが分かります。同じ漸化式が、Gerlachの方法と比べてずっと簡単に求められます。また、この方法とSecant法とのかかわりについては、別の機会に述べさせていただきます。
m=2の場合
漸化式は、次のようになります。
m=3の場合
漸化式は、次のようになります。
m=4の場合
漸化式は、次のようになります。
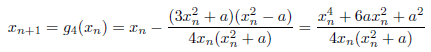
m=5の場合
漸化式は、次のようになります。
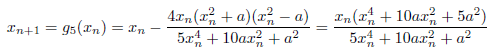
m=6の場合
漸化式は、次のようになります。
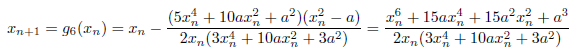
十進BASICによるプログラム
次に、十進BASICによるプログラム例を示します。
Gerlach.BAS
1: ! 2: ! 平方根を収束計算により求める。 3: ! 4: ! 入力 5: ! a : 平方根を求めたい数 6: ! m : 収束の次数(m = 2, 3, 4, 5, 6) 7: ! m=2:Newton, m=3:Halley 8: ! x0: 初期値 9: ! 10: OPTION ARITHMETIC DECIMAL_HIGH 11: DECLARE EXTERNAL FUNCTION iter 12: 13: INPUT PROMPT " 平方根を求めたい数 a = " : a 14: INPUT PROMPT " 収束の次数 m(2,3,4,5,6)= " : m 15: LET m = INT(m) 16: IF m < 2 THEN LET m = 2 17: IF m > 6 THEN LET m = 6 18: INPUT PROMPT " 初期値 x0 = " : x0 19: 20: LET i = 0 21: PRINT i, x0 22: DO 23: LET x = x0 24: LET x0 = iter(a, x0, m) 25: LET i = i + 1 26: PRINT i, x0 27: LOOP WHILE ABS(x - x0) > 1e-1000 28: END 29: 30: EXTERNAL FUNCTION iter(a, x, m) 31: OPTION ARITHMETIC DECIMAL_HIGH 32: SELECT CASE m 33: CASE 2 34: LET iter = (x + a / x) / 2 35: CASE 3 36: LET iter = x * (x^2 + 3 * a) / (3 * x^2 + a) 37: CASE 4 38: LET iter = (x^4 + 6 * a * x^2 + a^2) / 4 / x / (x^2 + a) 39: CASE 5 40: LET iter = x * (x^4 + 10 * a * x^2 + 5 * a^2) / (5 * x^4 + 10 * a * x^2 + a^2) 41: CASE 6 42: LET iter = (x^6 + 15 * a * x^4 + 15 * a^2 * x^2 + a^3) / 2 / x / (3 * x^4 + 10 * a * x^2 + 3 * a^2) 43: END SELECT 44: END FUNCTION